House Numbers in Java

In this section, we are going to learn about house numbers in Java. It is a number that is comprised of a cube whose size is s + 1. On this cube, we have a square pyramid number whose side is s. The following diagram depicts a house number.

Generally, a house number Hs is represented mathematically as: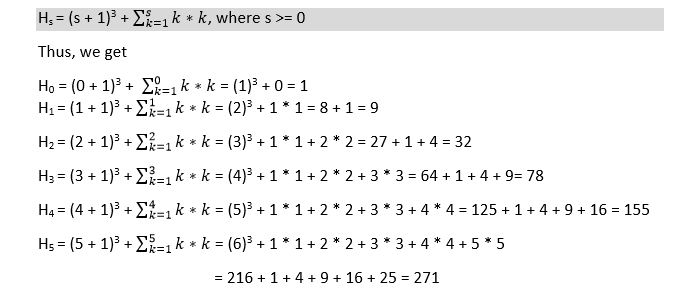

Implementation: Iterative

Let's see how one can implement the above-mentioned mathematical formula.

FileName: HouseNum.java

public class HouseNum
{
// a method to find the value of the house number
// located at the position s
public int findHouseNum(int s)
{
    // for s == 0
    // house number is always 1
    if(s == 0)
    {
        return 1;
    }
    
    int num = 0;
    
    // the mathematical formula has two parts
    // one is finding the value of (s + 1) ^ 3
    // another is finding the value of 1 ^ 2 + 2 ^ 2 + ... + s ^2
    
    // here we are computing the first part
    num = (s + 1) * (s + 1) * (s + 1);
    
    
    // here we are computing the second part
    for(int i = 1; i <= s; i++)
    {
    num = num + (i * i);
    }
    
    return num;
}

// main method
public static void main(String argvs[])
{
//creating an object of the class HouseNum
HouseNum obj = new HouseNum();

System.out.println("The first " + 10 + " house numbers are: ");
for(int i = 0; i < 10; i++)
{
System.out.print(obj.findHouseNum(i) + " ");   
}


}
}

Output:

The first 10 house numbers are: 
1 9 32 78 155 271 434 652 933 1285

Time complexity: The above program uses a loop to find the value of every house number. Therefore, the time complexity of the above program is O(n²), where n is the total number of house numbers one has to compute.

Implementation: Recursive

Using recursion also, one can also find the value of the house numbers. Observe the following program.

FileName: HouseNum1.java

public class HouseNum1
{
// a method that recursively finds the value of the house number
// located at the position s or t
public int findHouseNum(int s, int t)
{
    // the mathematical formula has two parts
    // one is finding the value of (s + 1) ^ 3
    // another is finding the value of 1 ^ 2 + 2 ^ 2 + ... + s ^2
    
    // for s == 0
    // house number is always 1
    if(s == 0)
    {
    // here we are computing the first part
     return (t + 1) * (t + 1) * (t + 1);
    }
    

    // recursively we are computing the value of 
    // 1 * 1 + 2 * 2 + ... + s * s
    return (s * s) + findHouseNum(s - 1, t);
}

// main method
public static void main(String argvs[])
{
//creating an object of the class HouseNum1
HouseNum1 obj = new HouseNum1();

System.out.println("The first " + 10 + " house numbers are: ");
for(int i = 0; i < 10; i++)
{
System.out.print(obj.findHouseNum(i, i) + " ");   
}


}
}

Output:

The first 10 house numbers are: 
1 9 32 78 155 271 434 652 933 1285

Time complexity: The above program is recursively finding the value of every house number. Therefore, the time complexity of the above program is O(n²), where n is the total number of house numbers one has to compute.

Optimized Implementation

The iteration or recursion we are using in the above two approaches to compute the value of the house numbers is the main culprit of increasing the time complexity. Therefore, we have to find a way to discard that iteration or recursion. For that, let's observe the mathematical formula again.

The recursion or iteration is happening because the summation we are doing in the second part. If we take a closer look, we will find that the second part is nothing but the summation of the square of the first s natural numbers. Therefore,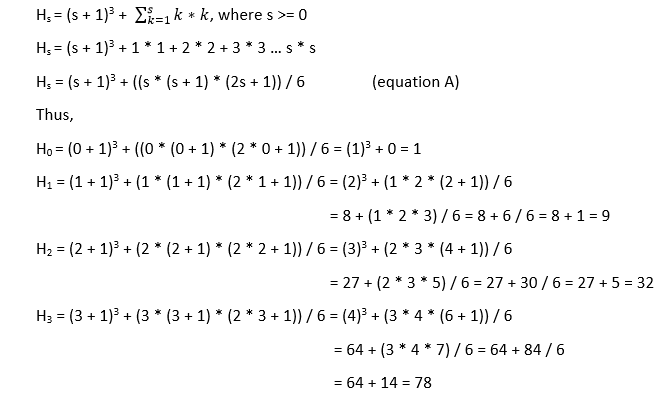

Let's implement the above compute mathematical formula.

FileName: HouseNume2.java

public class HouseNum2
{
// a method that finds the value of the house number
// located at the position s
public int findHouseNum(int s)
{
    // the mathematical formula has two parts
    // one is finding the value of (s + 1) ^ 3
    // another is finding the value of (s * (s + 1) * (2 * s + 1)) / 6
    
    // here we are computing the first part
    int num = (s + 1) * (s + 1) * (s + 1);
    
    // here we are computing the second part
    num = num + (s * (s + 1) * (2 * s + 1)) / 6;
    

    return num;
}

// main method
public static void main(String argvs[])
{
//creating an object of the class HouseNum2
HouseNum2 obj = new HouseNum2();

System.out.println("The first " + 10 + " house numbers are: ");
for(int i = 0; i < 10; i++)
{
System.out.print(obj.findHouseNum(i) + " ");   
}


}
}

Output:

The first 10 house numbers are: 
1 9 32 78 155 271 434 652 933 1285

Time complexity: The above program is not using any recursion or iteration to find the value of every house number. Therefore, the time complexity of the above program is O(n), where n is the total number of house numbers one has to compute.

The mathematical formula still has the first part ([s + 1]³), and the second part ([s * ( s + 1) * (2 * s + 1)] / 6). However, we can solve equation A to combine all these parts.

Thus,

H_s = (s + 1)³ + ((s * (s + 1) * (2s + 1)) / 6 ............. (equation A)

H_s = (s + 1)³ + ((s * (s + 1) * (2s + 1)) / 6

H_s = (s + 1) [(s + 1)² + (s * (2s + 1)) / 6]

H_s = (s + 1) [ s² + 2s + 1 + ((s² + s) * (2s + 1)) / 6]

H_s = (s + 1) [s² + 2s + 1 + (2s² + s) / 6]

H_s = (s + 1) [6s² + 12s + 6 + 2s² + s] / 6

H_s = (s + 1) [8s² + 13s + 6] / 6 = (8s³ + 13s² + 6s + 8s² + 13s + 6) / 6

H_s = (8s³ + 21s² + 19s + 6) / 6 ............. (equation B)

In equation B, all the terms have been combined and this equation can also be used to find the house numbers. The following program illustrates the same.

FileName: HouseNume3.java

public class HouseNum3
{
// a method that finds the value of the house number
// located at the position s
public int findHouseNum(int s)
{

    // Hs = (8 * s ^ 3 + 21 * s ^ 2 + 19 * s + 6) / 6 equation B 
    int num = ((8 * s * s * s) + (21 * s * s) + (19 * s) + 6) / 6;
    
    return num;
}

// main method
public static void main(String argvs[])
{
//creating an object of the class HouseNum3
HouseNum3 obj = new HouseNum3();

System.out.println("The first " + 10 + " house numbers are: ");
for(int i = 0; i < 10; i++)
{
System.out.print(obj.findHouseNum(i) + " ");   
}


}
}

Output:

The first 10 house numbers are: 
1 9 32 78 155 271 434 652 933 1285

Time complexity: The time complexity of the above program is still the same, i.e., O(n), as the program is not using any recursion or iteration to find the value of every house number. n is the total number of house numbers one has to compute.

Next TopicJava Program to Generate Binary Numbers

← prev next →