Huffman Coding Java

The Huffman Coding Algorithm was proposed by David A. Huffman in 1950. It is a lossless data compression mechanism. It is also known as data compression encoding. It is widely used in image (JPEG or JPG) compression. In this section, we will discuss the Huffman encoding and decoding, and also implement its algorithm in a Java program.

We know that each character is a sequence of 0's and 1's and stores using 8-bits. The mechanism is called fixed-length encoding because each character uses the same number of fixed-bit storage.

Here, a question ascends, is it possible to reduce the amount of space required to store a character?

Yes, it is possible by using variable-length encoding. In this mechanism, we exploit some characters that occur more frequently in comparison to other characters. In this encoding technique, we can represent the same piece of text or string by reducing the number of bits.

Huffman Encoding

Huffman encoding implements the following steps.

It assigns a variable-length code to all the given characters.
The code length of a character depends on how frequently it occurs in the given text or string.
A character gets the smallest code if it frequently occurs.
A character gets the largest code if it least occurs.

Huffman coding follows a prefix rule that prevents ambiguity while decoding. The rule also ensures that the code assigned to the character is not treated as a prefix of the code assigned to any other character.

There are the following two major steps involved in Huffman coding:

First, construct a Huffman tree from the given input string or characters or text.
Assign, a Huffman code to each character by traversing over the tree.

Let's brief the above two steps.

Huffman Tree

Step 1: For each character of the node, create a leaf node. The leaf node of a character contains the frequency of that character.

Step 2: Set all the nodes in sorted order according to their frequency.

Step 3: There may exist a condition in which two nodes may have the same frequency. In such a case, do the following:

Create a new internal node.
The frequency of the node will be the sum of the frequency of those two nodes that have the same frequency.
Mark the first node as the left child and another node as the right child of the newly created internal node.

Step 4: Repeat step 2 and 3 until all the node forms a single tree. Thus, we get a Huffman tree.

Huffman Encoding Example

Suppose, we have to encode string abracadabra. Determine the following:

Huffman code for All the characters
Average code length for the given String
Length of the encoded string

(i) Huffman Code for All the Characters

In order to determine the code for each character, first, we construct a Huffman tree.

Step 1: Make pairs of characters and their frequencies.

(a, 5), (b, 2), (c, 1), (d, 1), (r, 2)

Step 2: Sort pairs with respect to frequency, we get:

(c, 1), (d, 1), (b, 2) (r, 2), (a, 5)

Step 3: Pick the first two characters and join them under a parent node.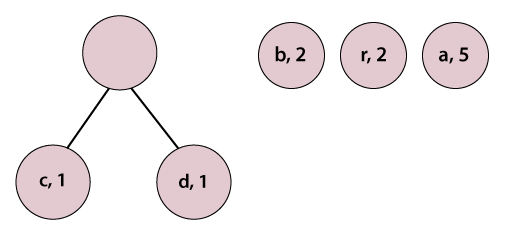

We observe that a parent node does not have a frequency so, we must assign a frequency to it. The parent node frequency will be the sum of its child nodes (left and right) i.e. 1+1=2.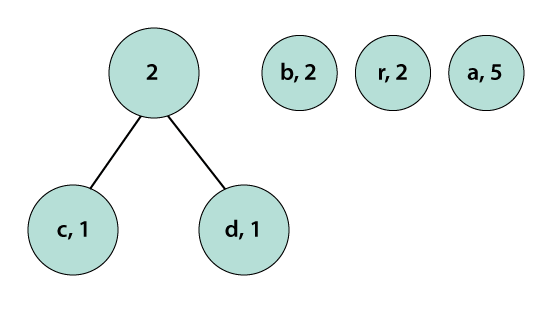

Step 4: Repeat Steps 2 and 3 until, we get a single tree.

We observe that the pairs are already in a sorted (by step 2) manner. Again, pick the first two pairs and join them.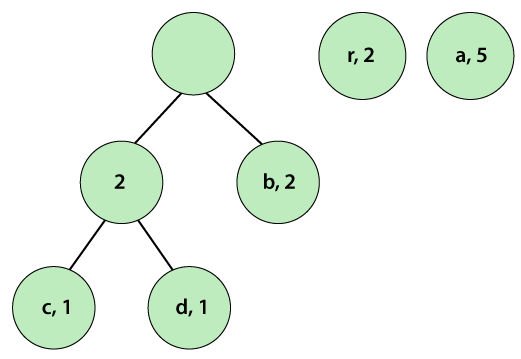

We observe that a parent node does not has a frequency so, we must assign a frequency to it. The parent node frequency will be the sum of its child nodes (left and right) i.e. 2+2=4.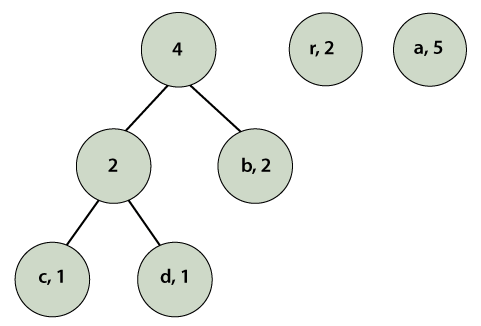

Again, we check if the pairs are in a sorted manner or not. At this step, we need to sort the pairs.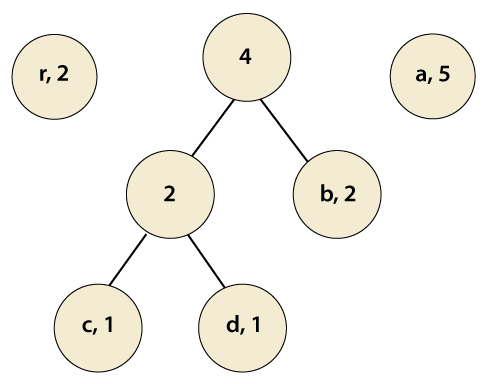

According to step 3, pick the first two pairs and join them, we get: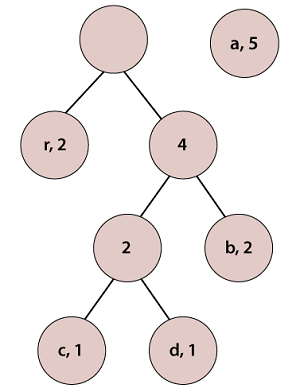

We observe that a parent node does not have a frequency so, we must assign a frequency to it. The parent node frequency will be the sum of its child nodes (left and right) i.e. 2+4=6.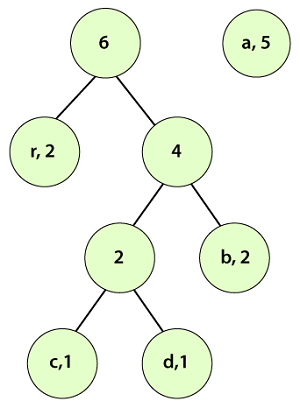

Again, we check if the pairs are in a sorted manner or not. At this step, we need to sort the pairs. After sorting the tree looks like the following: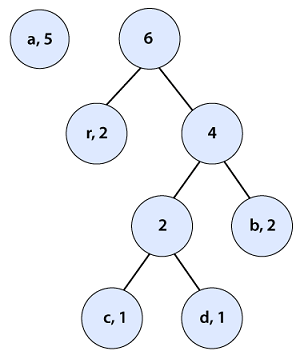

According to step 3, pick the first two pairs and join them, we get: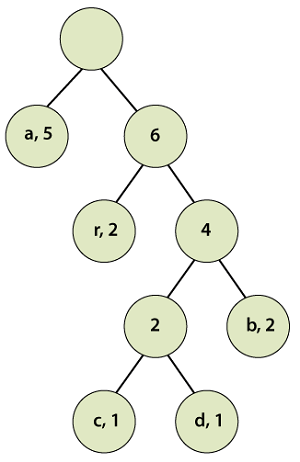

We observe that a parent node does not have a frequency so, we must assign a frequency to it. The parent node frequency will be the sum of its child nodes (left and right) i.e. 5+6=11.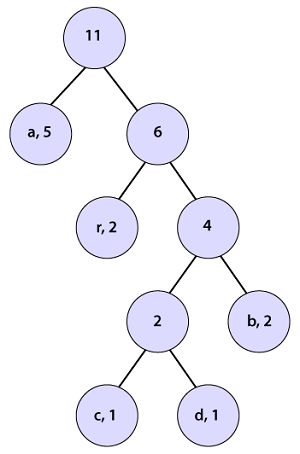

Therefore, we get a single tree.

At last, we will find the code for each character with the help of the above tree. Assign a weight to each edge. Note that each left edge-weighted is 0 and the right edge-weighted is 1.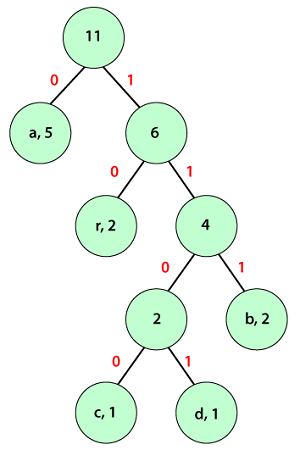

We observe that input characters are only presented in the leave nodes and the internal nodes have null values. In order to find the Huffman code for each character, traverse over the Huffman tree from the root node to the leaf node of that particular character for which we want to find code. The table describes the code and code length for each character.

Character	Frequency	Code	Code Length
A	5	0	1
B	2	111	3
C	1	1100	4
D	1	1101	4
R	2	10	2

We observe that the most frequent character gets the shortest code length and the less frequent character gets the largest code length.

Now we can encode the string (abracadabra) that we have taken above.

(ii) Average Code Length for the String

The average code length of the Huffman tree can be determined by using the formula given below:

= { (5 x 1) + (2 x 3) + (1 x 4) + (1 x 4) + (2 x 2) } / (5+2+1+1+2)

= 2.09090909

(iii) Length of the Encoded String

The length of the encoded message can be determined by using the following formula:

length= Total number of characters in the text x Average code length per character

= 11 x 2.09090909

= 23 bits

Huffman Encoding Algorithm

Huffman (C)
n=|C|
Q=C
for i=1 to n-1
    do
        z=allocate_Node()
        x=left[z]=Extract_Min(Q)
        y=right[z]=Extract_Min(Q)
        f[z]=f[x]+f[y]
Insert(Q,z)
return Extract_Min(Q)

The Huffman algorithm is a greedy algorithm. Since at every stage the algorithm looks for the best available options.

The time complexity of the Huffman encoding is O(nlogn). Where n is the number of characters in the given text.

Huffman Decoding

Huffman decoding is a technique that converts the encoded data into initial data. As we have seen in encoding, the Huffman tree is made for an input string and the characters are decoded based on their position in the tree. The decoding process is as follows:

Start traversing over the tree from the root node and search for the character.
If we move left in the binary tree, add 0 to the code.
If we move right in the binary tree, add 1 to the code.

The child node holds the input character. It is assigned the code formed by subsequent 0s and 1s. The time complexity of decoding a string is O(n), where n is the length of the string.

Huffman Encoding and Decoding Java Program

In the following program, we have used data structures like priority queues, stacks, and trees to design a compression and decompression logic. We will base our utilities on the widely used algorithmic technique of Huffman coding.

HuffmanCode.java

import java.util.Comparator;
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
//defining a class that creates nodes of the tree
class Node
{
    //storing character in ch variable of type character
    Character ch;
    //storing frequency in freq variable of type int
    Integer freq;
    //initially both child (left and right) are null
    Node left = null; 
    Node right = null; 
    //creating a constructor of the Node class
    Node(Character ch, Integer freq)
    {
        this.ch = ch;
        this.freq = freq;
    }
    //creating a constructor of the Node class
    public Node(Character ch, Integer freq, Node left, Node right)
    {
        this.ch = ch;
        this.freq = freq;
        this.left = left;
        this.right = right;
    }
}
//main class
public class HuffmanCode
{
	//function to build Huffman tree
	public static void createHuffmanTree(String text)
    {
        //base case: if user does not provides string
        if (text == null || text.length() == 0) 
        {
            return;
        }
        //count the frequency of appearance of each character and store it in a map
        //creating an instance of the Map 
        Map<Character, Integer> freq = new HashMap<>();
        //loop iterates over the string and converts the text into character array
        for (char c: text.toCharArray()) 
        {
        	//storing character and their frequency into Map by invoking the put() method 
            freq.put(c, freq.getOrDefault(c, 0) + 1);
        }
        //create a priority queue that stores current nodes of the Huffman tree.
        //here a point to note that the highest priority means the lowest frequency 
        PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(l -> l.freq));
        //loop iterate over the Map and returns a Set view of the mappings contained in this Map
        for (var entry: freq.entrySet()) 
        {
        	//creates a leaf node and add it to the queue
            pq.add(new Node(entry.getKey(), entry.getValue()));
        }
        //while loop runs until there is more than one node in the queue
        while (pq.size() != 1)
        {
            //removing the nodes having the highest priority (the lowest frequency) from the queue
            Node left = pq.poll();
            Node right = pq.poll();
            //create a new internal node with these two nodes as children and with a frequency equal to the sum of both nodes' frequencies. Add the new node to the priority queue.
            //sum up the frequency of the nodes (left and right) that we have deleted 
            int sum = left.freq + right.freq;
            //adding a new internal node (deleted nodes i.e. right and left) to the queue with a frequency that is equal to the sum of both nodes
            pq.add(new Node(null, sum, left, right));
        }
        //root stores pointer to the root of Huffman Tree
        Node root = pq.peek();
        //trace over the Huffman tree and store the Huffman codes in a map
        Map<Character, String> huffmanCode = new HashMap<>();
        encodeData(root, "", huffmanCode);
        //print the Huffman codes for the characters
        System.out.println("Huffman Codes of the characters are: " + huffmanCode);
        //prints the initial data
        System.out.println("The initial string is: " + text);
        //creating an instance of the StringBuilder class 
        StringBuilder sb = new StringBuilder();
        //loop iterate over the character array
        for (char c: text.toCharArray()) 
        {
        	//prints encoded string by getting characters 
            sb.append(huffmanCode.get(c));
        } 
        System.out.println("The encoded string is: " + sb);
        System.out.print("The decoded string is: ");
        if (isLeaf(root))
        {
            //special case: For input like a, aa, aaa, etc.
            while (root.freq-- > 0) 
            {
                System.out.print(root.ch);
            }
        }
        else 
        {
            //traverse over the Huffman tree again and this time, decode the encoded string
            int index = -1;
            while (index < sb.length() - 1) 
            {
                index = decodeData(root, index, sb);
            }
        }
    }
//traverse the Huffman Tree and store Huffman Codes in a Map
    //function that encodes the data
    public static void encodeData(Node root, String str, Map<Character, String> huffmanCode)
    {
        if (root == null) 
        {
            return;
        }
        //checks if the node is a leaf node or not
        if (isLeaf(root)) 
        {
            huffmanCode.put(root.ch, str.length() > 0 ? str : "1");
        }
        encodeData(root.left, str + '0', huffmanCode);
        encodeData(root.right, str + '1', huffmanCode);
    }
    //traverse the Huffman Tree and decode the encoded string function that decodes the encoded data
    public static int decodeData(Node root, int index, StringBuilder sb)
    {
        //checks if the root node is null or not
        if (root == null) 
        {
            return index;
        } 
        //checks if the node is a leaf node or not
        if (isLeaf(root))
        {
            System.out.print(root.ch);
            return index;
        }
        index++; 
        root = (sb.charAt(index) == '0') ? root.left : root.right;
        index = decodeData(root, index, sb);
        return index;
    }
    //function to check if the Huffman Tree contains a single node
    public static boolean isLeaf(Node root) 
    {
    	//returns true if both conditions return ture
        return root.left == null && root.right == null;
    }
    //driver code
    public static void main(String args[])
    {
        String text = "javatpoint";
        //function calling
        createHuffmanTree(text);
    }
}

Output:

Huffman Codes of the characters are: {p=000, a=110, t=111, v=001, i=010, j=011, n=100, o=101}
The initial string is: javatpoint
The encoded string is: 011110001110111000101010100111
The decoded string is: javatpoint

Next TopicJava Snippet Class

← prev next →