Insertion Sort in JavaWe can create a java program to sort array elements using insertion sort. Insertion is good for small elements only because it requires more time for sorting large number of elements. 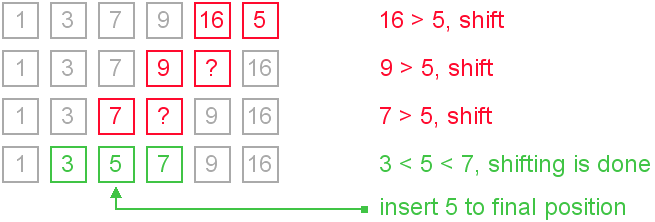
Let's see a simple java program to sort an array using insertion sort algorithm. Output: Before Insertion Sort 9 14 3 2 43 11 58 22 After Insertion Sort 2 3 9 11 14 22 43 58
Next TopicJava Programs
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










