Intersection Point of Two Linked List in JavaIn a system, two singly linked lists are given. By some mistake, the last node of one of the linked lists got linked to the second list. Thus creating a list a Y-shaped linked list. Our task is to find out the point where the given two linked lists merge. 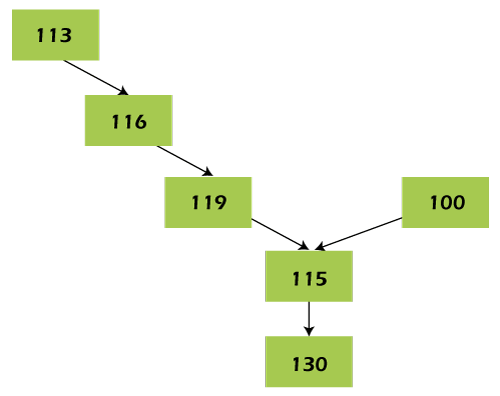
As per the above diagram, 115 is the intersection point of the two linked lists. Approach / Algorithm: Using Two LopsUsing the two nested for-loops, we can find the solution. The outer loop is dedicated to traversing the first list, and the inner loop is dedicated to the second list. For each iteration of the outer loop, traverse the second linked list completely, and check whether the node pointed in the outer loop is present in the linked list, which is traversed by the inner loop, or not. ImplementationObserve the implementation of the mentioned approach. FileName: LinkedListIntersection.java Output: The first linked list is: 113 116 119 115 130 The second linked list is: 110 115 130 The first intersection point of the linked lists is: 115 Complexity Analysis: The time complexity of the above program is O(m * n), where m is the total number of nodes present in the first linked list and n is the total number of nodes present in the second linked list. Since the program is not using any extra space, therefore, the space complexity of the program is O(1). Approach: Using Node CountStep 1: Count the number of nodes present in the first linked list, which is c1 in our case. Step 2: Count the number of nodes present in the second linked list, which is c2 in our case. Step 3: Find the difference between the count c1 and c2 and store it in a variable, diff in our case. Step 4: Start a loop from I = 0 to diff and start traversing the nodes of the first linked list till the value diff. Step 5: Now start traversing both the linked lists parallelly. When we get the common node, its value is returned. If null is reached, -1 can be returned, indicating that the two linked lists have no intersection point. ImplementationObserve the implementation of the mentioned algorithm. FileName: LinkedListIntersection.java Output: The first linked list is: 113 116 119 115 130 The second linked list is: 110 115 130 The first intersection point of the linked lists is: 115 Complexity Analysis: The time complexity of the above program is O(m + n), where m is the total number of nodes present in the first linked list and n is the total number of nodes present in the second linked list. Since the program is not using any extra space, therefore, the space complexity of the program is O(1). Approach: Using HashSetStep 1: Create a HashSet for storing the integers. Step 2: Start a loop for traversing the first linked list. Store all the nodes present in the first linked list in the HashSet, created in the first step. Step 3: Start a loop for traversing the second linked list. In each traversal, check whether the value of the node pointed in that traversal is present in the HashSet or not. If it is present, immediately terminate the loop and return that value. If the iteration of the loop is exhausted, then it means the intersection point of the linked list does not exist. ImplementationObserve the implementation of the mentioned algorithm. FileName: LinkedListIntersection.java Output: The first linked list is: 113 116 119 115 130 The second linked list is: 110 115 130 The first intersection point of the linked lists is: 115 Complexity Analysis: The time complexity of the program is the same as the above. The space complexity of the program is O(m), m is the total number of nodes present in the first list. It is because we are using a hash set for storing the value of the nodes of the first linked list. Approach: Using Two PointersStep 1: Initialize the two pointers p1 and p2 at the h1 and h2. Step 2: One node at a time, traverse through the list. Step 3: When p1 approaches the last of the list, then re-direct it to h2. Step 4: Similarly, when p2 approaches the last of the list, re-direct it to h1. Step 5: Once both of the linked lists go through the re-assigning, it will be the same distance from the point of collision. Step 6: If at any node pt1 coincides with p2, then it means that node is the intersection node. Step 7: After the second iteration, if there is no intersecting node, then return NULL. ImplementationObserve the implementation of the mentioned algorithm. FileName: LinkedListIntersection2.java Output: The first linked list is: 113 116 119 115 130 The second linked list is: 110 115 130 The first intersection point of the linked lists is: 115 Complexity Analysis: The time complexity of the program is the same as the above. The space complexity of the program is O(1), as the program is not using any extra space. Approach: Creating Circular First Linked ListStep 1: Start a loop for traversing the first linked list. Go till the last node of the first linked list. While traversing, count the number of nodes present in the linked list, and store it in a variable, which is countNode in our case. Also, store the last node of the linked list in a variable. Step 2: Now, link the last node of the list to the first node of the list. Thus, making a circular linked list (loop in the linked list). Step 3: As the length of the first linked list is already known, traverse that number of nodes in the second linked list using a pointer, which is p2 in our case. Step 4: Begin another pointer from the head of the second linked list (h2). Step 5: Move h2 and p2 by one node at a time using a loop. The terminating condition of the loop should be (p2 != h2). When the p2 and h2 meet, that point is the first intersection point of the given two linked list. Step 6: Make the last node of the first linked list point to null. In this way, the first linked list regains its original state by removing the loop in the linked list. ImplementationObserve the implementation of the mentioned algorithm. FileName: LinkedListIntersection3.java Output: The first linked list is: 113 116 119 115 130 The second linked list is: 110 115 130 The first intersection point of the linked lists is: 115 Complexity Analysis: The complexity analysis of the program is the same as the above. Approach: Using Mathematical EquationStep 1: Start a loop for traversing the first linked list in order to compute the count of nodes. Store the count in a variable, which is s1 in our case. Step 2: Start a loop for traversing the second linked list in order to compute the count of nodes. Store the count in a variable, which is s2 in our case. Also, store the last node of the linked list in a variable, which is l1 in our case. Step 3: Now, reverse the first linked list using a loop. Step 4: Start a loop for traversing the second linked list in order to compute the count of nodes. Store the count in a variable, which is s3 in our case. Also, store the last node of the linked list in a variable, which is l2 in our case. Step 5: Compare the addresses stored in l2 and l1. If they are same, then both the linked lists are not intersecting. If they are the same, go to the next step. Step 6: The total size of the common nodes of the linked list is (s1 + s2 - s3) / 2. Store this value in a variable, which is y in our case. Step 7: Now, traverse (s2 - y) number of nodes in the second linked list using a loop. The current position of the pointer gives the intersection point of the two linked lists. Step 8: Reverse the first linked list again to reinstate the changes. ImplementationObserve the implementation of the mentioned algorithm. FileName: LinkedListIntersection3.java Output: The first linked list is: 113 116 119 115 130 The second linked list is: 110 115 130 The first intersection point of the linked lists is: 115 Complexity Analysis: The complexity analysis of the program is the same as the above.
Next TopicSparse Number in Java
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










