Invert a Binary tree in Java

Inverting or mirroring a binary tree is common in computer science and programming. It reverses the arrangement of left and right subtrees at each node, effectively creating a mirror image of the original tree.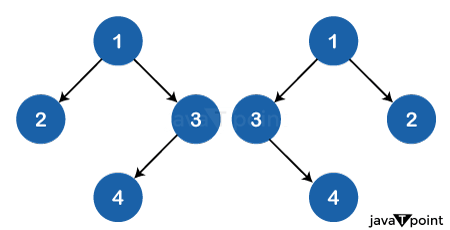

The process essentially mirrors the tree across its vertical axis. In binary tree manipulation, inversion is a frequently used operation that plays a key role in optimizing various algorithms related to trees. The concept involves recursively navigating the tree and exchanging the positions of the left and right children for each node.

Approach: Recursive Tree Traversal

Recursive Tree Traversal is a method used to explore and process a tree-like structure's nodes (or boxes). The approach involves breaking down the task of navigating the tree into smaller, more manageable steps.

Algorithm:

Step 1: Create a BinaryTreeNode class representing a binary tree point. It has a number (value), a left child, and a right child. It also has a way to start with a value when it's created.

Step 2: Make a class called BinaryTreeMirrorConverter that will help us change a binary tree to its mirror image. The class has a variable called root that points to the starting point of the tree.

Step 3: Inside BinaryTreeMirrorConverter, make a method called convertToMirror. It just changes the root to whatever the result is when we use a helper method.

Step 4: Make a helper method called convertToMirror. It takes a point in the tree (a node) and does the following:

If the point is empty (null), say it's empty.
If not, change the left and right parts of the point by calling this method for each of them, and then swap them.
Finally, return the updated point.

Step 5: Inside BinaryTreeMirrorConverter, make a method called inorderTraversal. It helps us go through the tree in a specific order.

Step 6: Make a helper method called inorderTraversal. It takes a point in the tree (a node) and if the point isn't empty, go to the left, print the value, and then go to the right.

Step 7: In the main part of our program, create a new BinaryTreeMirrorConverter named tree. Build a tree with some numbers in a specific order. Show the numbers in the tree in a certain order (inorder traversal). Change the tree to its mirror. Show the numbers in the mirrored tree in the same order.

Implementation

Filename: BinaryTreeMirrorConverter.java

// Define a class representing a node in a binary tree
class BinaryTreeNode {
    int value;                // Value of the node
    BinaryTreeNode leftChild;  // Reference to the left child node
    BinaryTreeNode rightChild; // Reference to the right child node

    // Constructor to initialize a binary tree node with a given value
    public BinaryTreeNode(int item) {
        value = item;
        leftChild = rightChild = null; // Initialize left and right child references to null
    }
}

// Define a class for converting a binary tree to its mirror
public class BinaryTreeMirrorConverter {
    BinaryTreeNode root; // Reference to the root node of the binary tree

    //Method to convert the binary tree to its mirror
    void convertToMirror() {
        root = convertToMirror(root);
    }

    // Recursive Method to convert a binary tree node to its mirror
    BinaryTreeNode convertToMirror(BinaryTreeNode currentNode) {
        if (currentNode == null)
            return currentNode; // If the node is null, return it as is

        // Recursively convert left and right subtrees
        BinaryTreeNode leftSubtree = convertToMirror(currentNode.leftChild);
        BinaryTreeNode rightSubtree = convertToMirror(currentNode.rightChild);

        // Swap left and right subtrees
        currentNode.leftChild = rightSubtree;
        currentNode.rightChild = leftSubtree;

        return currentNode; // Return the current node with swapped subtrees
    }

    // Method to perform inorder traversal of the binary tree
    void inorderTraversal() {
        inorderTraversal(root);
    }

    // Recursive Method to perform inorder traversal
    void inorderTraversal(BinaryTreeNode currentNode) {
        if (currentNode == null)
            return; // If the node is null, do nothing

        // Traverse left subtree
        inorderTraversal(currentNode.leftChild);

        // Print current node's value
        System.out.print(currentNode.value + " ");

        // Traverse right subtree
        inorderTraversal(currentNode.rightChild);
    }

    // Main Method to test the BinaryTreeMirrorConverter class
    public static void main(String args[]) {
        // Create an instance of BinaryTreeMirrorConverter
        BinaryTreeMirrorConverter tree = new BinaryTreeMirrorConverter();

        // Constructing the original binary tree
        tree.root = new BinaryTreeNode(1);
        tree.root.leftChild = new BinaryTreeNode(2);
        tree.root.rightChild = new BinaryTreeNode(3);
        tree.root.leftChild.leftChild = new BinaryTreeNode(4);
        tree.root.leftChild.rightChild = new BinaryTreeNode(5);

        // Print inorder traversal of the original tree
        System.out.println("Inorder traversal of the original tree:");
        tree.inorderTraversal();
        System.out.println("\n");

        // Convert the original tree to its mirror
        tree.convertToMirror();

        // Print inorder traversal of the mirrored tree
        System.out.println("Inorder traversal of the mirrored tree:");
        tree.inorderTraversal();
    }
}

Output:

Inorder traversal of the original tree:
4 2 5 1 3 
Inorder traversal of the mirrored tree:
3 1 5 2 4

Time Complexity: The time complexity is O(n), where n is the number of nodes in the binary tree. Each node is visited once during the mirror conversion process.

Auxiliary Space: The auxiliary space complexity is O(h), where h is the height of the binary tree. The recursion stack space contributes to the auxiliary space.

Approach: Level Order Traversal

Level Order Traversal is a tree traversal algorithm that visits nodes level by level, from left to right, starting from the root of the tree. The approach employs a queue to manage the order of node exploration, enqueuing the root initially.

Algorithm:

Step 1: Define a class TreeNode with attributes int data, TreeNode left, and TreeNode right.

Step 2: Define a class BinaryTree with static methods.

Step 3: In the main Method, create a sample binary tree.

Step 4: Print the inorder traversal of the original binary tree.

Step 5: Call the convertToMirror method with the root of the binary tree.

Step 6: Inside convertToMirror:

Use a queue for level order traversal.
Swap left and right children at each node.
Enqueue left and right children if they exist.

Step 7: Print the inorder traversal of the mirrored binary tree.

Implementation:

Filename: BinaryTree.java

import java.util.*;
public class BinaryTree {
    // Class representing a node in a binary tree
    static class TreeNode {
        int data;         // Value of the node
        TreeNode left;    // Reference to the left child node
        TreeNode right;   // Reference to the right child node
    }
    // Helper method to create a new node with the given data
    static TreeNode createNewNode(int data) {
        TreeNode node = new TreeNode();
        node.data = data;
        node.left = node.right = null;
        return (node);
    }

    // Method to convert a binary tree to its mirror image
    static void convertToMirror(TreeNode root) {
        if (root == null)
            return;

        // Use a queue for level order traversal
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        // Perform BFS. Swap left and right children at each node
        while (!queue.isEmpty()) {
            TreeNode current = queue.poll();

            // Swap left child with right child
            TreeNode temp = current.left;
            current.left = current.right;
            current.right = temp;

            // Enqueue the left and right children if they exist
            if (current.left != null)
                queue.add(current.left);
            if (current.right != null)
                queue.add(current.right);
        }
    }

    // Helper method to perform Inorder traversal and print node values
    static void printInorderTraversal(TreeNode node) {
        if (node == null)
            return;
        printInorderTraversal(node.left);
        System.out.print(node.data + " ");  // Print the value of the current node
        printInorderTraversal(node.right);
    }

    // Main method to demonstrate the functionality
    public static void main(String args[]) {
        // Creating a sample binary tree
        TreeNode root = createNewNode(1);
        root.left = createNewNode(2);
        root.right = createNewNode(3);
        root.left.left = createNewNode(4);
        root.left.right = createNewNode(5);

        // Displaying the original binary tree
        System.out.println("Original Binary Tree (Inorder Traversal):");
        printInorderTraversal(root);
        System.out.println();

        // Convert the binary tree to its mirror image
        convertToMirror(root);

        // Displaying the mirrored binary tree
        System.out.println("Mirrored Binary Tree (Inorder Traversal - Mirror Image):");
        printInorderTraversal(root);
    }
}

Output:

Original Binary Tree (Inorder Traversal):
4 2 5 1 3 
Mirrored Binary Tree (Inorder Traversal - Mirror Image):
3 1 5 2 4

Time Complexity: The time complexity is O(n), where n is the number of nodes in the binary tree. It is because each node is visited once during the level order traversal.

Auxiliary Space: The auxiliary space complexity is O(w), where w is the binary tree's maximum width (number of nodes at any level).

Next TopicJava Template Engine

← prev next →