Java Binary to Hexadecimal Conversion

In programming, converting one type to/ from a type is a crucial task. Sometimes we require, conversion from one type to another type. In the Java conversion section, we have discoed various types of conversions. In this section, we can discuss how to convert binary to hexadecimal in Java.

Hexadecimal Number

As the name suggests Hexadecimal number comprises 16 entities with 10 digits (0-9) that represent the first 10 hexadecimal numbers and the rest six entities represented by A to F (represented by the numbers 10 to 15). Note that the lowest number in the hexadecimal number system is 0 and the highest number is 15 which is represented by F.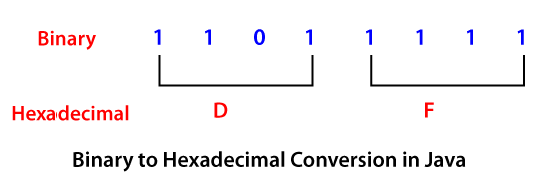

In the above example, we have broken the binary number 11011111 into chunks of 4 bits such as 1101 and 1111 that act as two characters (D and F) for the corresponding hexadecimal number.

Java Programs to Convert Binary to Hexadecimal

There are the following two ways to convert Binary to Hexadecimal in Java:

• Using Integer.toHexString() Method
• Get the remainder and divide the converted decimal number by 16

Using Integer.toHexString() Method

In the following Java program, we have defined two functions one that reads the number and the second that converts the number from binary to hexadecimal. In the get() function, first, we have converted the given number into an integer. For converting the binary number to a hexadecimal number, we have invoked toHexString() method of the Integer class.

Syntax:

The method accepts an integer to convert to a string. It returns the corresponding hexadecimal string.

BinaryToHexadecimal1.java

Output 1:

Enter the number: 11111
Hexadecimal Value is: 1f

Output 2:

Enter the number: 11001100
Hexadecimal Value is: cc

Let's see another approach for the same.

Algorithm

1. Convert the given binary number into a decimal number (first, extract each digit using by getting the remainder by dividing the number by 10).
2. Multiply this digit with increasing powers of 2.
3. Repeatedly divide the given binary number by 10 which eliminates the last digit in each iteration.
4. After getting the decimal number, use the toHexString() method to get the hexadecimal string as a result.

Let's understand the above steps through an example.

Example

Suppose, the given binary number is 01011011. First we will convert it to the decimal number by using the Math.pow() method and decrement the length. Therefore,

01011011 = (0 × 2⁷) + (1 × 2⁶) + (0 × 2⁵) + (1 × 2⁴) + (1 × 2³) + (0 × 2²) + (1 × 2¹) + (1 × 2⁰)

= (0 × 128) + (1 × 64) + (0 × 32) + (1 × 16) + (1 × 8) + (0 × 4) + (1 × 2) + (1 × 1)

= 0 + 64 + 0 + 16 + 8 + 0 + 2 + 1

= 91 (01011011 in decimal)

Now, we will convert the decimal number (91) to a hexadecimal number. Compare the decimal number with 16. It is greater, so we will divide the decimal number by 16.

91÷16, we get 5 as quotient, and 11 as remainder. Again, we compare remainder (11) with 16 which is less than 16.

Hence hexadecimal number of remainder (11) is B. That is,

91 = 16 × 5 +11 = B

5 = 16 × 0 + 5 = 5

= 5B (hexadecimal of 01011011)

Let's implement the above steps in a Java program.

BinaryToHexadecimal2.java

Output:

Binary Number: 1100110011
Hexadecimal Number: 9E

Let's see the above approach using an if-else statement.

BinaryToHexadecimal3.java

Output:

Enter the Binary Number: 1110001110
The respective Hexadecimal number is: 38E