Java Program to Add Digits Until the Number Becomes a Single Digit Number

In this section, we will create Java programs that add digits of a number until the number becomes a single-digit number. The problem is also known as the digit root problem.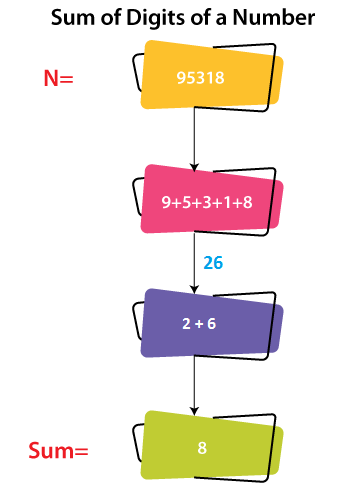

Example

Suppose, 76345 is a number for which we have to find the sum until it becomes a single-digit number.

7 + 6 + 3 + 4 + 5 = 25

Further, we will add 2 and 5.

2 + 5 = 7

We get 7 as a single-digit number.

Brute Force Approach

• Calculate the sum of all digits.
• Make a recursive call with the sum (calculated in the above step).
• If the number is less than 10, return the number.

Let's implement the above logic in a Java program.

SingleDigit.java

Output:

The sum of digits is: 1

We can also solve the above problem without using any loop and recursion. The approach is as follows:

In this approach, first, check if the number is divisible by 9 or not. If divisible, add the digits together and check if the sum is divisible by the number 9 or not. If divisible, the number is divisible by 9, else not.

For example, 54 i.e. (5 + 4 = 9). We get 9 as the sum of digits. Hence, the sum is divisible by 9.

We observe that if a number (n) is divisible by 9, then sum up its digit until the sum becomes a single digit which is always 9. For example:

n = 2880

Sum of digits = 2 + 8 + 8 + 0 = 18

The number 18 further can be added to form a single digit number.

18 = 1 + 8 = 9

The answer is always 9, if a number has the form like 9x. If the number is of the form 9x+k

A number can be of the form 9x or 9x + k. For the first case, the answer is always 9. For the second case, the answer is always k which is the remainder.

• If number is 0, return 0.
• Find remainder of number with 9. (number%9).
• If remainder is 0, return 9 else return remainder.

Let's implement the above approach in a Java program.

SumOfDigits.java

Output:

The sum of digits is: 2

The above approach solves the problem in O(1) time. Another approach that solves the problem in O(1) is as follows: