Java Program to Find GCD of Two Numbers

In this section, we have covered different logics in Java programs to find GCD of two numbers.

Greatest Common Divisor: It is the highest number that completely divides two or more numbers. It is abbreviated for GCD. It is also known as the Greatest Common Factor (GCF) and the Highest Common Factor (HCF). It is used to simplify the fractions.

How to Find the Greatest Common Factor

Write all the factors of each number.
Select the common factors.
Select the greatest number, as GCF.

Example: Find the GCF of 12 and 8.

Solution:

Factors of 12: 1, 2, 3, 4, 6, 12

Factors of 8: 1, 2, 4, 8

Common Factors: 1, 2, 4

Greatest Common Factor: 4

Hence, the GCF of 12 and 8 is 4.

Algorithm to Find GCD

Declare two variables, say x and y.
Run a loop for x and y from 1 to max of x and y.
Check that the number divides both (x and y) numbers completely or not. If divides completely store it in a variable.
Divide the stored number.

In Java, we can use the following ways to find the GCD of two numbers:

Using Java for loop
Using while loop
Using User-Defined Method
Using the Euclidean Algorithm
Using Modulo Operator

Using Java for loop

In the following program, we have initialized two numbers x=12 and y=8. After that, we have used a for loop that runs from 1 to the smallest of both numbers. It executes until the condition i <= x && i <= y returns true. Inside the for loop, we have also used if statement that tests the condition (x%i==0 && y%i==0) and returns true if both conditions are satisfied. At last, we have store the value of i in the variable gcd and print the same gcd variable.

FindGCDExample1.java

public class FindGCDExample1 
{
public static void main(String[] args) 
{
//x and y are the numbers to find the GCF
int x = 12, y = 8, gcd = 1;
//running loop form 1 to the smallest of both numbers
for(int i = 1; i <= x && i <= y; i++)
{
//returns true if both conditions are satisfied 
if(x%i==0 && y%i==0)
//storing the variable i in the variable gcd
gcd = i;
}
//prints the gcd
System.out.printf("GCD of %d and %d is: %d", x, y, gcd);
}
}

Output:

GCD of 12 and 8 is: 4

Using Java while Loop

In the following example, we have used while loop to test the condition. The loop executes until the condition n1!=n2 becomes false.

FindGCDExample2.java

public class FindGCDExample2
{
public static void main(String[] args) 
{
int n1=50, n2=60;
while(n1!=n2) 
{
if(n1>n2)
n1=n1-n2;
else
n2=n2-n1;
}
System.out.printf("GCD of n1 and n2 is: " +n2);
}
}

Output:

GCD of n1 and n2 is: 10

In the above program, we can replace the while loop with the following logic that gives the same output.

FindGCDExample3.java

public class FindGCDExample3
{
public static void main(String[] args) 
{
int Num1=12, Num2=8, Temp, GCD=0;
while(Num2 != 0)
{
Temp = Num2;
Num2 = Num1 % Num2;
Num1 = Temp;
}
GCD = Num1;
System.out.println("\n GCD =  " + GCD);
}
}

Output:

GCD =  4

Using User-Defined Method

In the following program, we have defined a method named findGCD(). It contains the logic to find the GCD of two numbers. We have parsed two parameters a and b of type int.

FindGCDExample4.java

import java.util.Scanner;
public class FindGCDExample4
{
//private static Scanner sc;
public static void main(String[] args) 
{
int a, b, gcd = 0;
Scanner sc = new Scanner(System.in);
System.out.print("Enter the First Number: ");
a = sc.nextInt();	
System.out.print("Enter the Second Number: ");
b = sc.nextInt();
gcd = findGCD(a, b);
System.out.println("GCD of " + a + " and " + b + " =  " + gcd);
}
public static int findGCD(int a, int b)
{
while(b != 0)
{
if(a > b)
{
a = a - b;
}
else
{
b = b - a;
}
}
return a;
}
}

Output:

Enter the First Number: 75
Enter the Second Number: 125
GCD of 75 and 125 = 25

Using the Euclidean Algorithm

The Euclidean Algorithm is an efficient method to compute GCD of two numbers. It is also known as Euclid's Algorithm. The algorithm states that:

If A=0 then GCD(A,B)=B, since the GCD(0,B)=B, and we can exit from the algorithm.
If B=0 then GCD(A,B)=A, since the GCD(A,0)=A, and we can exit from the algorithm.
Write A in the quotient that we get from (A=B*Q+R).

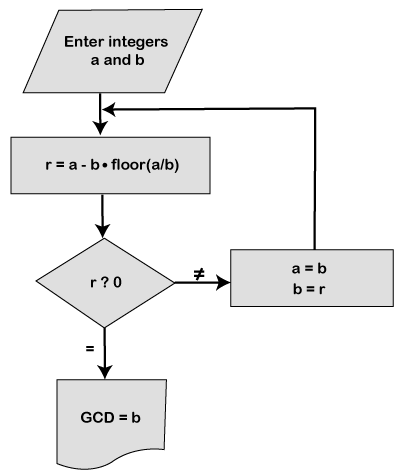
Java Program to Break Integer into Digits

Let's implement the above logic in a Java program.

FindGCDExample5.java

import java.util.Scanner;
public class FindGCDExample5
{
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
System.out.println("Enter the two numbers: ");
int x = sc.nextInt();
int y = sc.nextInt();
System.out.println("The GCD of two numbers is: " + findGCD(x,y));
}
static int findGCD(int x, int y)
{
int r=0, a, b;
a = (x > y) ? x : y; // a is greater number
b = (x < y) ? x : y; // b is smaller number
r = b;
while(a % b != 0)
{
r = a % b;
a = b;
b = r;
}
return r;
}
}

Output:

Enter the two numbers: 
11
33
The GCD of two numbers is: 11

Using Modulo Operator

In the following program, we have defined a recursive function named findGCD(). It parses two parameters a and b of type int. If the second number (b) is equal to 0, the method returns a as GCD, else returns a%b.

FindGCDExample6.java

public class FindGCDExample6
{ 
public static void main(String[] args) 
{ 
int a = 112, b = 543; 
System.out.println("GCD of " + a +" and " + b + " is " + findGCD(a, b)); 
}
//recursive function to return gcd of a and b 
static int findGCD(int a, int b) 
{ 
if (b == 0) 
return a; 	
return findGCD(b, a % b); 
} 
}

Output:

GCD of 112 and 543 is 1

Let's see another logic to find the GCD of two numbers.

FindGCDExample7.java

public class FindGCDExample7
{ 
public static void main(String[] args) 
{ 
int a = 54, b = 24; 
System.out.println("GCD of " + a +" and " + b + " is " + gcd(a, b)); 
} 
//recursive function to return gcd of a and b 
static int gcd(int a, int b) 
{ 
// Everything divides 0 
if (a == 0) 
return b; 
if (b == 0) 
return a; 
if (a == b) 
return a; 
if (a > b) 
return gcd(a-b, b); 
return gcd(a, b-a); 
} 
}

Output: