Java Program to Solve Quadratic Equation

In algebra, a quadratic equation is an equation that can be reordered in standard form. The standard form of a quadratic equation is ax²+bx+c=0. It is also known as the second-degree equation. In this section, first will discuss the quadratic equation after that we will create Java programs to solve the quadratic equation by using different approaches.

In the equation ax²+bx+c=0, a, b, and c are unknown values and a cannot be 0. x is an unknown variable. The formula to find the roots of the quadratic equation is known as the quadratic formula.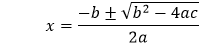

Java Program to Solve Quadratic Equation

A quadratic equation has two roots and the roots depend on the discriminant. In the above formula, (√b²-4ac) is called discriminant (d). The value of d may be positive, negative, or zero.

If d is positive (d>0), the root will be:

If the value of d is positive, both roots are real and different. It means there are two real solutions.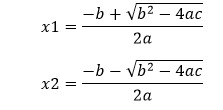

If d is zero (d=0), the root will be:

If the value of d is zero, both roots are real and the same. It means we get one real solution.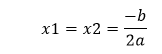

If d is negative (d<0), the root will be:

If the value of d is negative, both roots are distinct and imaginary or complex. It means that there are two complex solutions.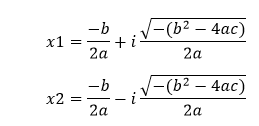

Algorithm to Find the Roots of the Quadratic Equation

Step 1: Start

Step 2: Read a, b, c

Step 3: initialize d<-(b*b)-(4*a*c)

Step 4: initialize r<- b/2*a

Step 5: if d>0 go to Step 6, else go to Step 8

Step 6: r1=r+(sqrt(d)/2*a) and r2=r-(sqrt(d)/2*a)

Step 7: prints roots are real and distinct, first root r1 second root r2

Step 8: if d=0 go to Step 9, else go to Step 10

Step 9: print roots are real and equal, -r

Step 10: d=-d

Step 11: im=sqrt(d)/2*a

Step 12: print roots are imaginary, first root is r+i im, and the second root is r-i im

Step 13: Stop

Let's create a Java program and implement the above steps.

Using if-else

QuadraticEquationExample1.java

import j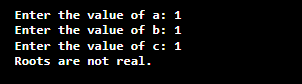ava.util.Scanner;
public class QuadraticEquationExample1
{
public static void main(String[] Strings) 
{
Scanner input = new Scanner(System.in);
System.out.print("Enter the value of a: ");
double a = input.nextDouble();
System.out.print("Enter the value of b: ");
double b = input.nextDouble();
System.out.print("Enter the value of c: ");
double c = input.nextDouble();
double d= b * b - 4.0 * a * c;
if (d> 0.0) 
{
double r1 = (-b + Math.pow(d, 0.5)) / (2.0 * a);
double r2 = (-b - Math.pow(d, 0.5)) / (2.0 * a);
System.out.println("The roots are " + r1 + " and " + r2);
} 
else if (d == 0.0) 
{
double r1 = -b / (2.0 * a);
System.out.println("The root is " + r1);
} 
else 
{
System.out.println("Roots are not real.");
}
}
}

Output 1:

Output 2: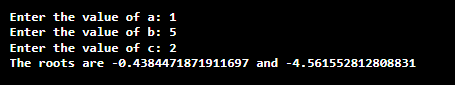

Using Function

QuadraticEquationExample2.java

import static java.lang.Math.*;
public class QuadraticEquationExample2
{
//defining a static method that finds the roots of the quadratic equation
static void calculateRoots(int a, int b, int c)
{
//comparing the value of a with 0, if a is 0 then the equation is not quadratic 
if (a == 0) 
{
System.out.println("The value of a cannot be 0.");
return;
}
//calculating discriminant (d)
int d = b * b - 4 * a * c;
double sqrtval = sqrt(abs(d));
if (d > 0) 
{
System.out.println("The roots of the equation are real and different. \n");
System.out.println((double)(-b + sqrtval) / (2 * a) + "\n"+ (double)(-b - sqrtval) / (2 * a));
}
else if (d == 0) 
{
System.out.println("The roots of the equation are real and same. \n");
System.out.println(-(double)b / (2 * a) + "\n"+ -(double)b / (2 * a));
}
// executes if d < 0
else 
{
System.out.println("The roots of the equation are complex and different. \n");
System.out.println(-(double)b / (2 * a) + " + i"+ sqrtval + "\n"+ -(double)b / (2 * a)+ " - i" + sqrtval);
}
}
//main method
public static void main(String args[])
{
//Output 1
int a = 1, b = 5, c = 2;    
//calling function
calculateRoots(a, b, c);
//Output 2: int a=1, b=1, c=1             
//Output 3: int a=1, b=-2, c=1
}
}

Output 1: