Java Programming Challenges

Java programming challenges are complex problems that we have to solve through logic and implement that logic in any programming language. Solving programming challenges develops logical thinking, analytical skill. If you are preparing for interviews, you must solve these programming challenges once. It is advisable to first understand the problem and derive your solution or approach before directly moving to the solution.

In this section, we will discuss some of the most important programming challenges that are frequently asked in interviews phase-2 round i.e. coding round.

Fitting Shelves Problem
Assign Mice to Holes
Coin Change Problem
Count Maximum Point on a Line
Gold Bar Problem

Note: A problem can be solved in multiple ways, so the logic and method may differ from other solution or approach. Throughout this section, we have used the Java programming language to solve the problem.

Let's solve the challanges one by one.

Fitting Shelves Problem

Problem Statement:

It is given that the length of the wall is 'w' and the lengths of the two shelves is 'm' and 'n', respectively. It is required to find the number of each type of shelves that must be used to cover the wall with minimum empty space left. The larger of the two shelves is cheaper in price and is hence preferrable over the other. However, the priority is to minimize the empty space.

Let us understand the problem statement with an example.

Example:

Suppose that the length of the wall is 7 m (w = 7), length of the 1^st shelf is 3 m (m = 3), and the length of the 2^nd shelf is 5 m (n = 5). We need to find the number of shelves of type 1 and type 2. Let that number by x and y respectively.

Solving the problem mathematically, following equation can be formulated:

7 = 3x + 2y

To solve such equations, we perform hit and trial method.

The best optimal solution is the 3^rd one, where x = 1 and y = 2 because of the two reasons:

Empty space is zero.
2^nd shelf which is of larger length and cheaper cost is more in units. Hence, the cost factor is also considered.

3 * 1 + 2 * 2 = 7

Empty space = 7 - 7 = 0 (Length of the wall - (total length of 1^st and 2^nd shelf))

Let's take another set of values:

w = 29, m = 3, n = 9

29 = 3x + 9y

0 * 3 + 3 * 9 = 27

X = 0, Y = 3

Empty size = 29 - 27 = 2

Let's take another set of values:

w = 24, m = 4, n = 7

24 = 4x + 7y

6 * 4 + 0 * 7 = 24

X = 6, Y = 0

Empty size = 24 - 24 = 0

Here a point to note that the constraint that larger shelf costs less than the smaller one, starting from 0, we increase no of larger type shelves till they can be fit. In each case the empty space is calculated and finally store that value which minimizes the empty space. If the empty space is same in the two cases, we prefer the one with number of larger shelves.

FittingShelves.java

public class FittingShelves{
    // w is the length of the wall
    // m is the length of the first shelf
    // n is the length of the second shelf
    static void shelves( int w, int m, int n )
    {
        // Assuming m is always smaller than n
        // x is the number of shelves of m length
        // y is the number of shelves of n length
        // emp is the number of remaining spaces
        // Keeping y = 0 and solving the equation so formed (as in the above example) for x, the values shall be initialized as follows
        // empty spaces can be calculated as the remainder of the division of length of wall and length of 1st shelf for which we calculated the value of x
        int x = w / m, y = 0, emp = w % m, min_emp = w ;
        // storing the values of x, y and emp
        int num1 = x, num2 = y ;
        min_emp = emp ;        
        // maximum value of n can-not be more than the length of the wall 'w', therefore iterating the loop uptil the value of w
        while ( w >= n ) 
        {
            // incrementing the value of y to calculate x against different values of y (1, 2, 3, ...)
            y += 1 ;
            w = w - n ;
            // calculating the value of x. In the remaining part, any number of shelves of length can be placed
            x = w / m ;
            emp = w % m ;
            if( emp <= min_emp)
            {
                num1 = x ;
                num2 = y ; 
                min_emp = emp ;
            }
        }
        // printing the values on console
        System.out.println( " X : " + num1 + " Y : " + num2 + " Empty Space : " + min_emp ) ;
    }
    public static void main( String[ ] args )
    {
        // initializing the values 
        int w = 24, m = 3, n = 5 ;
        // calling the function ' shelves ' with the above values
        shelves( w, m, n ) ; 
        // initializing different set of values
        w = 7 ;
        m = 3 ;
        n = 5 ;
        // calling the function 'shelves' with the above values
        shelves( w, m, n ) ;
    }
}

Output:

X : 3 Y : 3 Empty Space : 0
X : 2 Y : 0 Empty Space : 1

Assign Mice to Holes

Problem Statement:

There are x mice and x holes placed in a straight line. Each hole can accommodate only 1 mouse. The position of the mouse is such that it can stay at his position or move towards right one step from x to x + 1, or move towards left one step from x to x - 1. It takes only 1 minute to follow any of these moves. Assign mice to holes so that the time when the last mouse gets inside a hole is minimized.

Examples:

Suppose the mice have the following positions: 4, -4, 2 and holes have 4, 0, 5 positions. We need to assign mice to holes in such a way that the time consumed in the entire process is minimized.

For ease of understanding, let's create two arrays, one holding positions of mice and another holding positions of holes.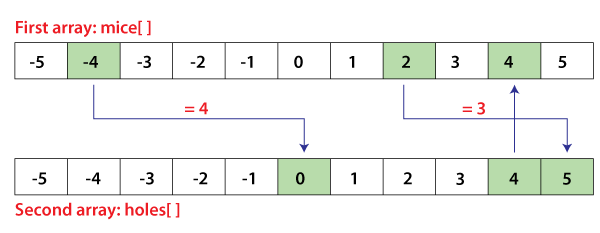

To compute the time taken by mouse to travel from its respective position to the position of the holes, we simply traverse the positions that lie in between. In simple words, we subtract the positions of mice and holes.

Case 1: Where mice travels from position 4 to the position 4 of the holes

Time: 4 - 4 = 0

Case 2: Where mice travels from position -4 to the position 0 of the holes

Time: 0 - (-4) = 0

Case 3: Where mice travels from position 2 to the position 5 of the holes

Time: 5 - 2 = 3

Clearly, the maximum time among the computed times is 4. Hence it can be said that it will take minimum 4 minutes to assign all mice to holes.

The problem can be resolved using a greedy approach. We can minimize time to put each mouse in the nearest hole. It can be performed by sorting the position of the mouse and the hole. Through this, we can put the mouse in the appropriate hole in the hole list. We can then find the maximum difference between the mouse and the corresponding position of the opening.

Algorithm:

Sort the positions of the mice in ascending order preferably.
Sort the positions of the holes
Loop i = 1 to N: Update answers according to the value of |mice(i) - hole(i)|. It should be maximum of all differences.
Let i1 < i2 be the positions of two mice and let j1 < j2 be the positions of two holes.

max(|i1- j1|, |i2 - j2|) <= max(|i1 - j2|, |i2 - j1|),

where '|a - b|' represent absolute value of (a - b).

MiceHoles.java

import java.util.* ;   
public class MiceHoles
{ 
    /* this function computes minimum time required to place the mice to a hole and returns the same */
    public int Holes( ArrayList< Integer > mice, ArrayList< Integer > holes ) 
    { 
        /* check if the size of mice and holes is same or not as this is a constraint of the question */
        if ( mice.size( ) != holes.size( ) ) 
           return -1 ; 
        // sorting the list of mice and holes in an ascending order
        Collections.sort( mice ) ; 
        Collections.sort( holes ) ;    
        int size = mice.size( ) ; 
        /* computing the difference between the mice and holes at each position as per our solution explained in the example */
        int max = 0 ;         
        for ( int i = 0; i < size; i++ ) 
        /* using the abs function of the math class to print the positive or absolute value */
            if ( max < Math.abs( mice.get( i ) - holes.get( i ) ) ) 
                max = Math.abs( mice.get( i ) - holes.get( i ) ) ; 
  
        // returning the computed ' max ' value
        return Math.abs( max ) ; 
    } 
    public static void main( String[ ] args ) 
    { 
        miceHoles mH = new miceHoles( ) ;         
        // creating any array list of type integer
        ArrayList< Integer > mice = new ArrayList< Integer >( ) ; 
        // adding the values in the arraylist using the add( ) method
        mice.add( 5 ) ; 
        mice.add( 2 ) ; 
        mice.add( 3 ) ; 
        // creating another array list of type integer
        ArrayList< Integer > holes = new ArrayList< Integer >( ) ; 
        holes.add( 4 ) ; 
        holes.add( 0 ) ; 
        holes.add( 5 ) ; 
        System.out.println( " The last mouse gets into" + 
         " the hole in time : " + mH.Holes( mice, holes ) ) ; 
    } 
}

Output:

The last mouse gets into the hole in time: 2

Coin Change Problem

Given a value N, if we want to make change for N cents, and we have infinite supply of each cent C = {C1, C2, …., Cm} valued coins. In how many ways can we make the change? The order of coins doesn't matter.

Example 1:

Let total sum be N = 5 and the types of coins C = {1, 2}

For the given values, the possible changes must be arranged keep in mind that the sum of the change must be 5.

{1, 1, 1, 1, 1}

{1, 1, 1, 2}

{1, 2, 2}

We can generate 3 such ways where the cents can be rearranged to give the sum of 5. Hence, the output must be 3.

Example 2:

Let N = 4 and C = {1, 2, 3}

For the given values, the possible changes must be arranged keeping in mind that the sum of the change must be 5.

{1, 1, 1, 1}

{1, 1, 2}

{2, 2}

{1, 3}

We can generate 4 such ways where the cents can be rearranged to give the sum of 5. Hence, the output must be 4.

Now, to find the total count, we can divide the solution into sub-solutions of two sets:

The solution that contains at least the one (i - 1)^th type of coin (the last coin)
The solution that does not contain the (i - 1)^th type of coin (or the last coin)

So, we will need to create a function, let's say, totalWays(C[ ], i , n) which will count the total number of ways by counting the number of solutions and then we can return the sum of totalWays(C[ ], i - 1, n) and totalWays(C[ ], i, n - C[ i - 1 ]).

The problem has Optimal Substructure Property since we are able to solve the problem by dividing it into subproblems and solving them first.

Now, we will implement the solution of this Coin Change problem by using a recursive structure as mentioned above.

Algorithm: -

Here, we have given each coin of a given value that can come any number of times. It means that repetition is allowed in here and this is known as Unbounded Knapsack.

Now, we have two choices for a particular type of coin:

To include it
To exclude it

But we need to remember, the first one, i.e., inclusion process, is not for just once but we can include any type of coin and number of times until
N < 0.

So basically, if we are at the C[i-1] (i.e., the last coin), we can include as many instances of that coin (this is unbounded inclusion), i.e., calling totalWays(C, i , n - C[i-1]) till we get

n <= 0;

Then we move to the next type of coin, i.e., C[i-2].

But remember, after moving to the C[i-2] coin (the second last coin), we can't go back and cannot make any choices for C[ i - 1 ], i.e., totalWays(C, i - 1, n).

At the end, we have added the solution to two subproblems,
i.e., totalWays(C, i - 1, n) + totalWays(C , i , n - C[i-1]); which is the answer we are required to find.

CoinChange.java

class CoinChange
{
    //  creating a recursive function which returns the total count of all the possible 
    // ways we can get the sum n from the given coins

    //  C[ ] contains all the types of coins
    //  i is the count of types of coins
    //  n is the total sum given to us
    static int totalWays( int C[ ], int i, int n )
    {
        // If n is equals to 0 then we have 1 solution found
        // ( do not include any coin )
        if ( n == 0 )
            return 1 ;
        // If the n is less than 0 then solution doesn't exist as in this case the sum of 
        // coins have become greater than n itself and hence, not the solution 
       // so, return 0
        if ( n < 0 )
            return 0 ;
        // If we don't have coins ( C[ ] is empty ) but still have n greater than 0 
        // then also we don't have the solution, so return 0
        if ( i <= 0 && n >= 1 )
            return 0 ;
        // we return the count of total ways by adding: -
        // 1. the solution computed by including c[ i - 1 ] element ( i.e, last element )
        // 2. the solution computed by excluding C[ i - 1 ] element
        return totalWays( C, i - 1, n ) +
               totalWays( C, i, n - C[ i - 1 ] ) ;
    }
    public static void main( String args[ ] )
    {
        // arr[ ] contains all the types of coins that we need to use
        int arr[ ] = { 2, 3 } ;
        // m is the count of coins we need to use
        int i = arr.length ;
        // printing the result returned by calling the
        System.out.println( totalWays( arr, i, 6 ) ) ;
    }
}

Output:

The following is the recursion tree for the given inputs.

N = 6, C = {2, 3}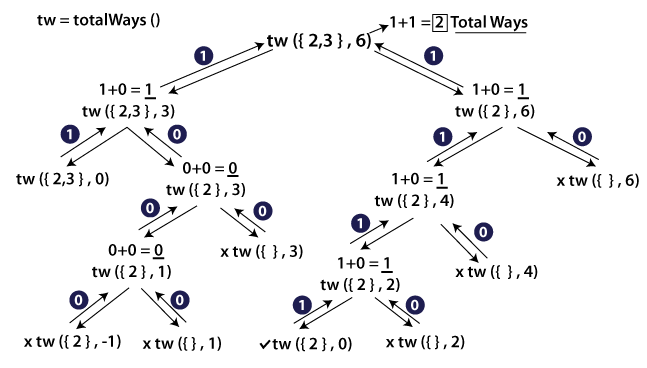

Count Maximum Point on A Line

Problem Statement:

Given N point on a 2D plane as pair of (x, y) co-ordinates, we need to find the maximum number of points which can lie on the same line.

Examples:

Input: points[ ] = { -3, 5 }, { 0, 0 }, { 1, 1 }, { 2, 2 }, { 3, 3 }, { 5, 8 }

The maximum number of points which lie on same line are {0, 0}, {1, 1}, {2, 2}, {3, 3}. Therefore, the count is 4.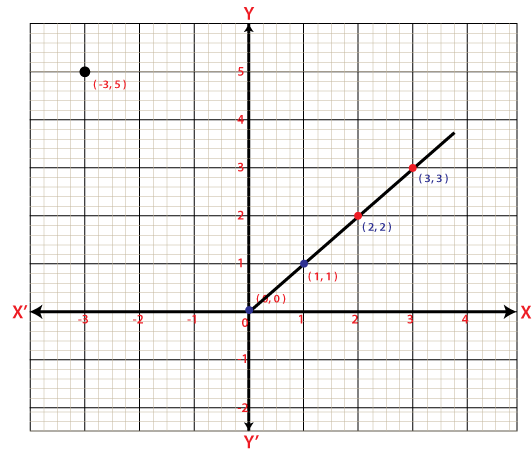

First take a point, say 'a', and then calculate its slope with respect to other points given to us. After that, we will use HashMap to record all the slopes and then check how many of them have the same slopes which will help us find out how many points are on the same line with 'a' being one of their points and finally updating the value of the 'count' which is the maximum number of points on the same line.

We will keep repeating this for every point and also keep updating the value of 'count' if we find any other line with a greater number of points on it than previously recorded.

Note: When we will find the slope by formula (y2 - y1) / (x2 - x1) we can encounter a problem when this results in a number less than '1' because in that case the slope will tend to be 0 (zero) which is not the correct answer. So, to overcome this we will use an inbuilt math function, i.e., "Math.atan", which will help us avoid this problem.

Time Complexity of this algorithm would be O(n²).

MaxPoint.java

import java.util.*;
class MaxPoint {
  // creating a function that takes in x-coordinates array
  // and y-coordinates array as int a[ ] and int b[ ] respectively
  // and returns the count of maximum points on a straight line
    public static int MaximumPoints( int s[ ], int t[ ] ) {  
    // initializing all the required values
    HashMap< Double, Integer > map = null ;
    int count = 0, ov = 0, same = 0, maximum_current = 0 ;
    double slope = 0, x, y ;
    // starting an outer loop which will iterate over 
    // x-coordinates, i.e., a[ i ]
    for ( int i = 0 ; I < s.length ; i++ ) {    
    // instantiating the HashMap which will be required
    // for recording every slope with respect to a 
    // pair of coordinates
      map = new HashMap< >( ) ;
      same = 0 ;
      count = 0 ;
      // starting the inner loop which will iterate over
      // y-coordinates, i.e. b[ j ]
      // setting j = i since we need not to find the slopes
      // for values that we've already found
      for( int j = i ; j < t.length ; j++ ) {        
        // if i == j  then they are a pair of coordinates ( x, y )
        // so, increment same as they will always be a part
        // of the coordinates on a same line
        if( i == j )
          same++ ;
        // else check if ( x2 - x1 is 0 )
        // and if 0 then we represent the infinity with
        // maximum integer value
        else{
          if( s[ j ] - s[ i ] == 0 ) {
          slope = Integer.MAX_VALUE ;
          continue ;
          }
          // here, we are calculating x = x2 - x1 
          // and y = y2 - y1 and then finally the slope
          // as ( y / x )          
          else {
            x = s[ j ] - s[ i ] ;
            y = t[ j ]- t[ i ] ;
            slope = Math.atan( y / x ) ; } 
            // if the map contains the slope as key already
            // then get the value of it and increment it and
            // again, store it back
            if( map.containsKey( slope ) ) {
              ov = map.get( slope ) ;
              map.put( slope, ov + 1 ) ;
            }   
            // else if the map doesn't contain the slope
            // then put this new key, value pair in the map 
            else map.put( slope, 1 ) ;
        }
      }
      // now, retrieving all the key, values from the map
      // and updating the new count value
      Set< Map.Entry< Double, Integer > > entries = map.entrySet( ) ;
        for( Map.Entry< Double, Integer > entry: entries ) {
          count = Math.max( count,entry.getValue( ) ) ;
        }
       // finally, updating the value of max_curr
       maximum_current = Math.max( maximum_current, count+same ) ;
    }
    return maximum_current ;
  }
  public static void main( String[ ] args ) {
  int count = 0 ;  
  // a[ ] is for x-coordinates
  // b[ ] is for y-coordinates
  int a[ ] = { -1, 0, 1, 2, 3, 3 } ;
  int b[ ] = { 1, 0, 1, 2, 3, 4 } ;
  count = MaximumPoints( a, b ) ;
  System.out.print( " Maximum points are " +count ) ;
  }
}

Output:

Maximum points are 4

Gold Bar Puzzle

Problem Statement:

A person is hired for seven days to work on the employer's house and as a compensation a gold bar is paid to him. The gold bar is divided into seven pieces and is connected with each other like a chain. A piece of gold is given to him at the end of everyday work. What and where are the minimum number of cuts to the chain of gold bar pieces will be made, so that you can pay him a piece of gold every day?

Solution:

In order to solve the problem, we will use a mathematical formula, i.e., 2ⁿ - 1.

Here, 'n' is a number ranging from '1' to 'x'.

And, 2^x - 1 should be less than total number of pieces of gold that we can have.

So, in our case, 2^x - 1 < 7, since the total gold bar pieces we can have, is 7.

We'll use the above approach to make cuts on the gold bar chain to have the minimum number of cuts to pay the person.

So, for the First cut 'n' is 1: -

2¹ - 1 => 2 - 1 = 1

Hence, we will make the first cut on the gold bar chain after the first segment, i.e., between first and second segment.

For the Second cut 'n' is 2: -

2² - 1 => 4 - 1 = 3

Hence, we'll make the second cut right after the third segment, i.e., between third and fourth segment on the gold bar. This leaves us with four segments without any cuts ( segment 4^th to 7^th).

Now, for the Third cut 'n' is 3: -

2³ - 1 => 8 - 1 = 7

Now, we know that 2ⁿ - 1 < 7, so this cut is not applicable.

So, the minimum number of cuts that we need to make on the gold bar would be 2 and these cuts will be made after 1^st segment (between 1^st and 2^nd gold bar segment) and 3^rd segment (between 3^rd and 4^th segment) of the gold bar.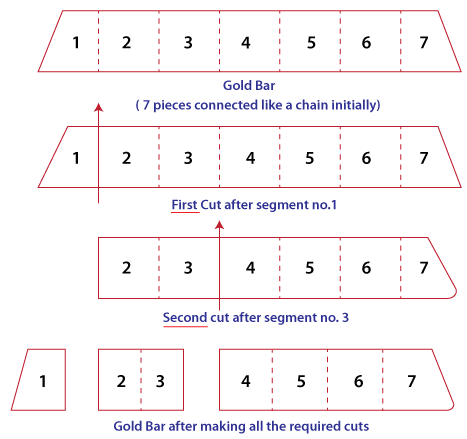

Explanation:

Let A = 1st segment (only 1 segment)

and B = 2nd and 3rd segment (2 segments)

and C = 4th till 7th segment (4 segments)

On Day 1 we will give the person A (i.e., the 1st segment).

On Day 2 we will give him B (i.e., 2 segments) while taking the A(1 segment) back from him. This leaves the person with 2 segments (B) at the end of 2nd Day.

On Day 3, we will give him again A. Now, he has A + B (i.e., total 3 segments).

On Day 4, we will give him C (4 segments) but will take back A and B. So, he has now 4 segments at the end of Day 4.

On Day 5, we will give him A.

On Day 6, we will give him B but will take back A. Now, he has C + B (i.e., 6 segments).

On the 7th Day, we will finally give him A and complete the puzzle.

GoldBarPuzzle.java

class GoldBarPuzzle {
    public static int cutsOnBar( int segments ) {
        int n = 0 ;
        int count = 1 ;
        while ( (Math.pow( 2, count ) - 1 ) < segments ) {
            n = n + 1 ;
            ++count ;
        }
        return n ;
    }
    public static void main( String[ ] args ) {
        int seg = 7 ;
        System.out.print( cutsOnBar( seg ) ) ;
    }
}

Output:

Next TopicJava URL Encoder

← prev next →