Kahn's algorithm for Topological Sorting in Java

Kahn's algorithm is a popular method used to perform topological sorting on a directed acyclic graph (DAG). Topological sorting is ordering the vertices in a DAG, such that for every directed edge (u, v), vertex u comes before vertex v in the ordering. In other words, there are no cycles in the sorted graph.

Multiple topological sortings are possible for a graph. For instance, the following graph can have two valid topological sortings: "5 4 2 3 1 0" and "4 5 2 0 3 1". In any valid topological sorting, the first vertex is always a vertex with an in-degree of 0, indicating it has no incoming edges from other vertices in the graph.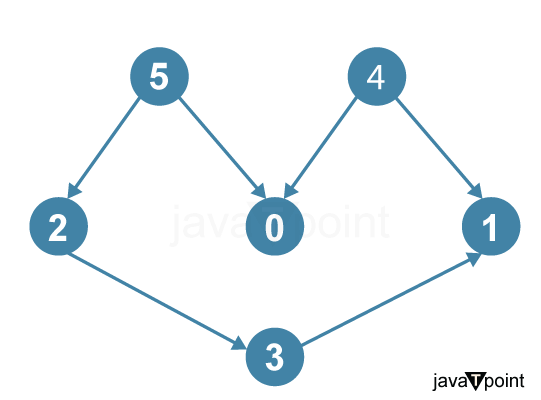

Kahn's algorithm for Topological Sorting in Java

Example:

Input: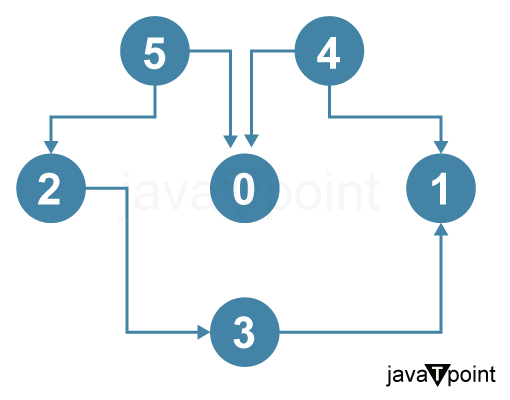

Output:

5 4 2 3 1 0

Explanation: Topological sorting of a directed acyclic graph (DAG) is a linear ordering of its vertices. For every directed edge uv, vertex u comes before v in the ordering. It means that for any vertex v, all its dependencies (vertices with edges directed into v) must come before v in the ordering.

In the example given, vertices 5 and 4 have no incoming edges, so they can be placed in any order in the topological ordering. The vertices 2 and 0 have incoming edges from 4 and 5, respectively, so they must come after 4 and 5 in the topological ordering. Finally, vertex 1 has no dependencies, so it must last in the topological ordering.

Example:

Input: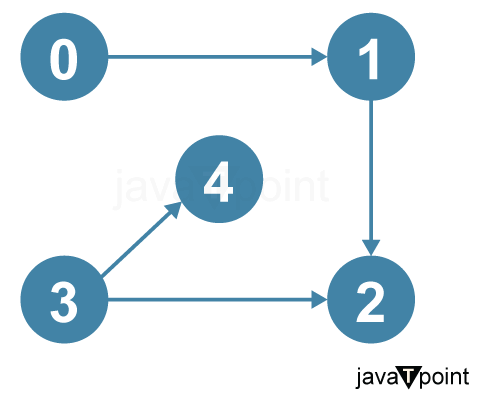

Output:

0 3 4 1 2

Explanation: In the directed acyclic graph (DAG), 0 and 3 have no incoming edges, 4 and 1 have incoming edges from 0 and 3, and 2 are placed at last.

Intuition:

The intuition behind topological sorting is that we can start with the vertices that have no dependencies and then add the vertices that depend on them. It ensures that we never add a vertex before its dependencies, which would create a cycle in the graph.

The nodes with outdegree 0 will always be our first preference to execute.
Then, after completing all of those tasks with 0 outdegrees, we will move on to tasks dependent on tasks that have already been handled (those tasks' outdegrees will now be 0), and so on for all other tasks.

The topological sorting algorithm is similar to a breadth-first search (BFS) but only adds vertices to the queue if they have indegree 0. It ensures that the vertices are added to the topological ordering in a dependency-ordered fashion.

Algorithm

Initialize a list of indegrees, where indegrees[i] is the number of edges that point to vertex i.
For each vertex i in the graph:
- Increment the indegrees of all vertices that are adjacent to i.
Create a queue and add all vertices with indegree 0 to the queue.
While the queue is not empty:
- Remove the first vertex from the queue and add it to the topological sorting list.
- For each vertex j that is adjacent to the removed vertex i:
  - Decrement the indegrees of j.
  - If the indegrees of j becomes 0, add j to the queue.
If the size of the topological sorting list is not equal to the number of vertices in the graph, then the graph contains a cycle, and the topological sorting algorithm returns an empty list.

How do we find the in-degree of each node?

The in-degree of a vertex is the number of edges that point to that vertex. In the code you provided, the in-degree of each vertex is calculated in the following for loop:

for (List<Integer> adjList : graph) {
    for (int dest : adjList) {
        indegrees[dest]++; // Increment indegree for each destination vertex
    }
}

The for loop iterates through all of the adjacency lists in the graph. For each adjacency list, it iterates through all of the destinations of the edges in the adjacency list. For each destination, it increments the indegree of the destination vertex. It ensures that the indegree of each vertex is correct after we have finished iterating through all of the adjacency lists.

Implementation:

Filename: TopologicalSort.java

import java.util.*;

public class TopologicalSort {
    public static void main(String[] args) {
        int numVertices = 6;
        List<List<Integer>> graph = new ArrayList<>();
        for (int i = 0; i < numVertices; i++) {
            graph.add(new ArrayList<>());
        }

        // Add edges to the graph
        addEdge(graph, 5, 2);
        addEdge(graph, 5, 0);
        addEdge(graph, 4, 0);
        addEdge(graph, 4, 1);
        addEdge(graph, 2, 3);
        addEdge(graph, 3, 1);

        // Perform topological sorting using indegrees
        List<Integer> topologicalSort = topologicalSort(graph);
        if (topologicalSort.isEmpty()) {
            System.out.println("Graph contains a cycle. Topological sorting not possible.");
        } else {
            System.out.println("Topological Sorting:");
            for (int vertex : topologicalSort) {
                System.out.print(vertex + " ");
            }
        }
    }

    // Method to add an edge from source to destination in the graph
    private static void addEdge(List<List<Integer>> graph, int src, int dest) {
        graph.get(src).add(dest); // Add dest to the adjacency list of src
    }

    // Method to perform topological sorting using indegrees
    private static List<Integer> topologicalSort(List<List<Integer>> graph) {
        int numVertices = graph.size();
        int[] indegrees = new int[numVertices];

        // Calculate indegrees of all vertices
        for (List<Integer> adjList : graph) {
            for (int dest : adjList) {
                indegrees[dest]++; // Increment indegree for each destination vertex
            }
        }

        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numVertices; i++) {
            if (indegrees[i] == 0) {
                queue.add(i); // Add vertices with indegree 0 to the queue as starting points for topological sorting
            }
        }

        List<Integer> result = new ArrayList<>();
        while (!queue.isEmpty()) {
            int vertex = queue.poll();
            result.add(vertex); // Add the current vertex to the result (topological sorting list)

            // Decrement indegree of adjacent vertices and add them to the queue if indegree becomes 0
            for (int dest : graph.get(vertex)) {
                indegrees[dest]--;
                if (indegrees[dest] == 0) {
                    queue.add(dest);
                }
            }
        }

        // If the graph contains a cycle, the size of the result list will be less than the number of vertices
        // In that case, return an empty list to indicate topological sorting is not possible.
        if (result.size() != numVertices) {
            result.clear();
        }

        return result;
    }
}

Output:

Topological Sorting:
4 5 2 0 3 1

Time Complexity: The time complexity of the code is O(V + E), where V is the number of vertices and E is the number of edges in the graph.

Auxiliary Space: The auxiliary space complexity is O(V), which comes from the additional data structures used in the algorithm.

Application of Kahn's algorithm for Topological Sort:

Course Sequencing: In educational institutions, students often need to follow a specific sequence of courses where certain courses serve as prerequisites for others. Kahn's algorithm can determine the order in which courses should be taken to ensure that all prerequisites are completed before enrolling in a particular course.
Management of Software Dependencies: In software development, applications often depend on external libraries or modules. Kahn's algorithm can manage these software dependencies by determining the correct linking order or loading the libraries, ensuring that each dependency is satisfied before the dependent code is executed.
Scheduling Tasks: Kahn's algorithm can be applied to schedule tasks in various domains, such as project management, job scheduling, or manufacturing processes. The algorithm helps determine the optimal order in which tasks should be executed to respect dependencies and improve efficiency.
Data Processing: In data processing pipelines, where various data processing steps depend on each other, Kahn's algorithm can establish the order in which the steps should be executed to avoid errors and ensure data consistency.
Circuit Design: In digital circuit design, certain logic gates or components may depend on the outputs of other gates. Kahn's algorithm can help designers determine the correct sequence of gate connections, ensuring that signals propagate correctly through the circuit.

Next TopicMost Popular Java Backend Tools

← prev next →