Keith Number in Java

In this section, we will learn what is Keith number and also create Java programs to check if the given number is Keith or not. The Keith number program frequently asked in Java coding test.

Keith Number

A positive n digit number X is called a Keith number (or repfigit number) if it is arranged in a special number sequence generated using its digits. The special sequence has first n terms as digits of x and other terms are recursively evaluated as the sum of previous n terms. For example, 197, 19, 742, 1537, etc.

Keith Number Example

Let's check the number 742 is a Keith number or not.

First, we will separate each digit, as 7, 4, 2

To find the next term of the above-created series, we add these digits (i.e. 7+4+2), and the resultant (13) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13

To find the next term of the above series, we add the last three terms (i.e. 13+2+4), and the resultant (19) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13, 19

To find the next term of the above series, we add the last three terms (i.e. 19+13+2), and the resultant (34) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13, 19, 34

To find the next term of the above series, we add the last three terms (i.e. 34+19+13), and the resultant (66) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13, 19, 34, 66

To find the next term of the above series, we add the last three terms (i.e. 66+34+19), and the resultant (119) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13, 19, 34, 66, 119

To find the next term of the above series, we add the last three terms (i.e. 119+66+34), and the resultant (219) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13, 19, 34, 66, 119, 219

To find the next term of the above series, we add the last three terms (i.e. 219+119+66), and the resultant (404) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13, 19, 34, 66, 119, 219, 404

To find the next term of the above series, we add the last three terms (i.e. 404+219+119), and the resultant (742) that we get becomes the next term of the series.

Now, the series becomes, 7, 4, 2, 13, 19, 34, 66, 119, 219, 404, 742

Here, we will stop the process because we get the same number (742) as a term of the series. Hence, the given number 742 is a Keith number.

From the above example, we observe that we need to calculate the terms of the series until we get the same number (that we have taken in starting) as a term of the series.

Note: If the given number (X) has n number of digits, we will recursively add the last n terms of the series. As the number 742 has three digits, so, we have added the last three terms of the series, each time.

Let's take another example.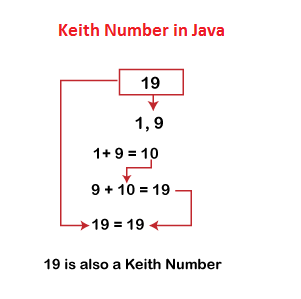

Steps to Find Keith Number

Read or initialize a number (X).
Separate each digit from the given number (X).
Add all the n-digits. It gives the next term of the series.
Again, add the last n-terms of the series to find the next term.
Repeat step 4 until we get the term the same as the number we have taken.

Let's implement the above steps in a Java program.

Keith Number Java Program

The logic is not much difficult. Compute the series using the sum of n previous numbers where n is the number of digits. If one of the numbers computed in the series is the same as the input number, it is a Keith number. The program stops if the value computed is greater than the input number.

Let's create a Java program and implement the above logic into it.

KeithNumberExample1.java

import java.util.*;
class KeithNumberExample1
{
//user-defined function that checks if the given number is Keith or not
static boolean isKeith(int x)
{
//List stores all the digits of the X
ArrayList<Integer> terms=new ArrayList<Integer>();
//n denotes the number of digits 
int temp = x, n = 0; 
//executes until the condition becomes false
while (temp > 0)
{
//determines the last digit of the number and add it to the List	
terms.add(temp%10);
//removes the last digit
temp = temp/10;
//increments the number of digits (n) by 1
n++;
}
//reverse the List
Collections.reverse(terms);
int next_term = 0, i = n;
//finds next term for the series
//loop executes until the condition returns true
while (next_term < x)
{
next_term = 0;
//next term is the sum of previous n terms (it depends on number of digits the number has)
for (int j=1; j<=n; j++)
next_term = next_term + terms.get(i-j);
terms.add(next_term);
i++;
}
//when the control comes out of the while loop, there will be two conditions:
//either next_term will be equal to x or greater than x
//if equal, the given number is Keith, else not
return (next_term == x);
}
//driver code
public static void main(String[] args)
{
//calling the user-defined method inside the if statement and print the result accordingly 	
if (isKeith(19))
System.out.println("Yes, the given number is a Keith number.");
else
System.out.println("No, the given number is not a Keith number.");
if(isKeith(742))
System.out.println("Yes, the given number is a Keith number.");
else
System.out.println("No, the given number is not a Keith number.");
if(isKeith(4578))
System.out.println("Yes, the given number is a Keith number.");
else
System.out.println("No, the given number is not a Keith number.");
}
}

Output:

Yes, the given number is a Keith number.
Yes, the given number is a Keith number.
No, the given number is not a Keith number.

Let's create another Java program to find all the Keith numbers that contain the same number of digits.

KeithNumberExample2.java

import java.util.Scanner;
public class KeithNumberExample2
{
public static void main(String args[]) 
{
Scanner sc= new Scanner(System.in);
System.out.print("Enter the number of digits the series must have: "); 
//reads an integer as length of the number from the user
int numlen = sc.nextInt();
//checks if the length of the number is greater than 2 or not
if (numlen < 2) 
{
//prints if the above condition returns false    
System.out.println("The number must have at least 2 digits.");
} 
//executes if the above condition returns true
else 
{
//calculates the lower bound from where the series starts
long lowBound = (long) Math.pow(10, numlen - 1);
//calculates the upper bound from where the series ends
long upperBound = (long) Math.pow(10, numlen);
for (long l = lowBound; l < upperBound; l++) 
{
if (isKeith(String.valueOf(l))) 
{
//prints all the Keith number between given range    
System.out.print(l + ", ");
}
}
}
sc.close();
}
//function that checks whether the given number is Keith or not
public static boolean isKeith(String input) 
{
int numlen = input.length();
//keep track only the last three terms
long[] series = new long[numlen];
for (int i = 0; i < numlen; i++) 
{
series[i] = Long.valueOf(input.substring(i, i + 1));
}
long next_term = 0;
long number = Long.valueOf(input);
while (next_term < number) 
{
next_term = 0;  
//calculates next term of the series
for (int i = 0; i < numlen; i++) 
{
next_term = next_term + series[i];
if (i < numlen - 1) 
{
//shift series to the left    
series[i] = series[i + 1]; 
} 
else 
{
//add new value to the series    
series[i] = next_term; 
}
}
//compares the next term of the series with the number and returns boolean value accordingly
if (next_term == number) 
{
return true;
}
}
return false;
}
}

Output 1:

Output 2:

Similarly, we can find the d-digit Keith numbers. The following table summarizes the d-digits Keith numbers.

d	d-digit Keith Numbers
2	14, 19, 28, 47, 61, 75
3	197, 742
4	1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909
5	31331, 34285, 34348, 55604, 62662, 86935, 93993
6	120284, 129106, 147640, 156146, 174680, 183186, 298320, 355419, 694280, 925993
7	1084051, 7913837
8	11436171, 33445755, 44121607
9	129572008, 251133297
10	(none)
11	24769286411 96189170155
12	171570159070, 202366307758, 239143607789, 296658839738
13	1934197506555, 8756963649152
14	43520999798747, 74596893730427, 97295849958669
15	120984833091531, 270585509032586, 754788753590897
16	3621344088074041, 3756915124022254, 4362827422508274
17	11812665388886672, 14508137312404344, 16402582054271374, 69953250322018194, 73583709853303061
18	119115440241433462, 166308721919462318, 301273478581322148
19	1362353777290081176, 3389041747878384662, 5710594497265802190, 5776750370944624064, 6195637556095764016
20	12763314479461384279, 27847652577905793413, 45419266414495601903
21	855191324330802397989
22	7657230882259548723593
23	26842994422637112523337, 36899277593852609997403, 61333853602129819189668
24	229146413136585558461227
25	9838678687915198599200604