Knapsack Problem Java

One of the prominent combinatorial optimization problems is the Knapsack problem Java. The Knapsack problem has two categories.

0-1 Kanpsack Problem
Factorial Knapsack Problem

Let's discuss each of them.

0 - 1 Knapsack Problem

Given values and weights of n different items. One has to put these items in a knapsack of capacity C such that the knapsack has the maximum value. Also, the sum of weights of all the items present in the knapsack should not exceed the capacity C. Since it is a 0 - 1 knapsack problem; hence, splitting the item is not allowed, i.e., one can never break any given item, either do not pick it or pick it (0 - 1 property).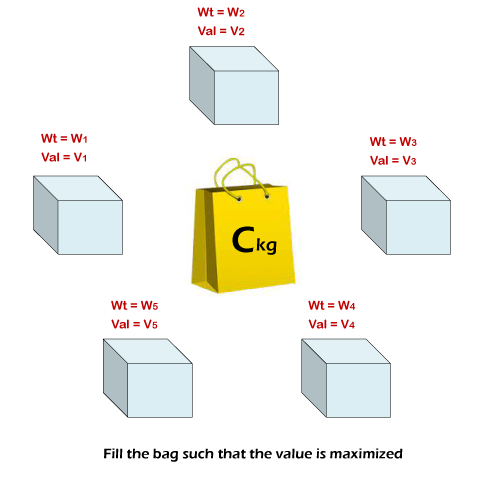

The knapsack problem can be solved either by using the exhaustive search or using dynamic programming.

Using Exhaustive Search

Exhaustive search means applying the brute force approach. In this approach, every set of items are tried, and for every set, the value is calculated. The set that generates the maximum value is the answer.

The following program implements the brute force approach using recursion.

FileName: KnapsackExample.java

// A recursive implementation
// of the 0 - 1 Knapsack problem 
public class KnapsackExample
{
// A utility method, which returns
// the maximum of the two numbers a1 and a2
public int max(int a1, int a2)
{
return (a1 > a2) ? a1 : a2;
}
// A method that returns the maximum value that
// may be put in the given knapsack of
// capacity c by applying brute force with the help of recursion
public int maxknapSackVal(int C, int wt[], int v[], int l)
{
// handling Base Case
if (l == 0 || C == 0)
{
    // if no item is present or 
    // the capacity of the knapsack is 0, 
    // then there is no need to go further. 
    return 0;
}
// The capacity C of the knapsack is less 
// than the lth item. Therefore, it is 
// not possible to include this item 
// in creating the solution
if (wt[l - 1] > C)
{
return maxknapSackVal(C, wt, v, l - 1);
}
else
{
// recursively solving the answer
// Case 1: include the lth item
int val1 = maxknapSackVal(C - wt[l - 1], wt, v, l - 1);
// Case 2: exclude the lth item
int val2 = maxknapSackVal(C, wt, v, l - 1);
// return the maximum of both 
return max(v[l - 1] + val1, val2);
}
}
// main method
public static void main(String argvs[])
{
// input arrays
int values[] = new int[] { 100, 60, 120 };
int weight[] = new int[] { 20, 10, 30 };
// capacity of the knapsack
int C = 50;
// calculating the length
int length = values.length;
// instantiating the class KnapsackExample
KnapsackExample knapObj = new KnapsackExample();
int maxVal = knapObj.maxknapSackVal(C, weight, values, length);
System.out.println("The maximum value is: " + maxVal);
}
}

Output:

The maximum value is: 220

Explanation: The input arrays are in such a way that their values are mapped, i.e., for item i, the weight is weight[i], and its value is values[i]. In each recursive call, there is a decision made whether the item should be included in the solution or not. If the item is not included, we move further without considering its value. If the item is included, then the capacity of the knapsack is reduced by the weight of the item, and we move further by including its value. Other items are treated in a similar way. The maximum value generated by adding the values of the included items gives our answer.

Note that the approach is not very conducive as it takes a lot of time to give the result. The time complexity of the approach is O(2 ^ n), where n is the number of elements present.

Using Dynamic Programming

The need of dynamic programming occurred because the above approach is taking a large amount of time to generate the result. Therefore, in the long run, the above method fails. Therefore, we need to look at another approach which is dynamic programming.

FileName: KnapsackExample1.java

// A solution for the 0 - 1 Knapsack problem
// using dynamic programming
public class KnapsackExample1
{
// A utility method, which returns
// the maximum of two integers a1 and a2
public int maximum(int a1, int a2)
{
	return (a1 > a2) ? a1 : a2;
}
// Returns the maximum value that can
// be put in a knapsack of capacity C
public int maxValueKnapsack(int C, int w[], int val[], int l)
{
int j, wt;
int dp[][] = new int[l + 1][C + 1];
// Filling the table dp[][] in the bottom-up manner
for (j = 0; j <= l; j++)
{
for (wt = 0; wt <= C; wt++)
{
if (j == 0 || wt == 0)
{
    // base case
	dp[j][wt] = 0;
}
else if (w[j - 1] <= wt)
{
    // similar the previous approach making two choices 
    // either exluding or including the items
    dp[j][wt] = maximum(val[j - 1] + dp[j - 1][wt - w[j - 1]], dp[j - 1][wt]);
}
else
{
    // current capacity of the knapsack does not allow 
    // this item. The current value is equal to the previous value
    dp[j][wt] = dp[j - 1][wt];
}
}
}
return dp[j - 1][C];
}
//  main method
public static void main(String argvs[])
{
// input arrays
int values[] = new int[] { 100, 60, 120 };
int weight[] = new int[] { 20, 10, 30 };
// capacity of the knapsack
int C = 50;
// length of the input arrays
int l = values.length;
// instantiating the class KnapsackExample
KnapsackExample knapObj = new KnapsackExample();
// invoking the method maxValueKnapsack()
int maxVal = knapObj.maxValueKnapsack(C, weight, values, l);
// displaying the final result
System.out.println("The maximum value is: " + maxVal);
}
}

Output:

The maximum value is: 220

Explanation: Similar to the first approach, this time also we are including and excluding every item present in the list. However, this time we are having a better time complexity of O(n^2). It is because, unlike the above approach, we are taking the help of the solution build for the smaller list of items to build the solution for the complete list of items (property of dynamic programming). Therefore, the number of iterations is less. Note that in both the approaches, we are completely excluding or including the items thus following the 0 - 1 property.

Fractional Knapsack Problem

The fractional knapsack problem is similar to the 0 - 1 knapsack problem. The only difference is one can choose an item partially. Thus, the liberty is given to break any item then put it in the knapsack, such that the total value of all the items (broken or not broken) present in the knapsack is maximized.

FileName: KnapsackExample1.java

// Java program to solve fractional Knapsack Problem
import java.util.Comparator;
import java.util.Arrays;
// the greedy approach
public class FractionalKnapSackExample
{
// method to get maximum value
private static double getMaxValue(int[] w, int[] v, int c)
{
// length of the array
int size = w.length;
// array of storing all the items
ItemValues[] iValue = new ItemValues[size];
for (int j = 0; j < size; j++) 
{
// storing the items
iValue[j] = new ItemValues(w[j], v[j], j);
}
// sorting the items on the basis of cost
Arrays.sort(iValue, new Comparator<ItemValues>() 
{
@Override
public int compare(ItemValues i1, ItemValues i2)
{
return i2.cost.compareTo(i1.cost);
}
});
// contains the maximum value that is possible 
// for the given capacity of the knapsack
double totalVal = 0d;
for (int j = 0; j < size; j++) 
{
// obtaining the current weight 
// and value of the ith item
int currWt = (int)iValue[j].w;
int currVal = (int)iValue[j].value;
if (c - currWt >= 0) 
{
// the current capacity of the knapsack allows the 
// item to be taken as a whole
c = c - currWt;
totalVal = totalVal + currVal;
}
else 
{
// when an item can not be picked as a whole
// we break the item and take a portion of it 
// such that we get the maximum value in the knapsack
double fraction	= ((double)c / (double)currWt);
totalVal = totalVal + (currVal * fraction);
c = (int)(c - (currWt * fraction));
// the knapsack is full 
// no need to proceed further
break;
}
}
return totalVal;
}
// Itemvalues class
static class ItemValues 
{
Double cost;
double w, value, index;
// item value function
public ItemValues(int w, int value, int index)
{
this.w = w;
this.value = value;
this.index = index;
// on the basis of cost 
// we sort the item
cost = new Double((double)value / (double)w);
}
}
// main method
public static void main(String argvs[])
{
// input arrays
int[] weight = { 40, 10, 20, 30 };
int[] values = { 40, 60, 100, 120 };
// capacity of the knapsack
int C = 50;
// invoking the getMaxValue() method        
double maxVal = getMaxValue(weight, values, C);
// printing the result
System.out.println("Maximum value that can be obtained is = " + maxVal);
}
}

Output:

Maximum value that can be obtained is = 240.0

Explanation: The greedy approach is used to solve the fractional knapsack problem. In this approach, we consider those items first which can give maximum value while consuming less weight. In other words, those items whose value / weight ratio is maximum. Therefore, we are sorting the list in non-decreasing order by taking the help of the value / weight ratio. Thus, the item with the highest value / weight ratio sits at the first index, the item with the second-highest value / weight ratio takes the second index, and so on.

Next TopicSession Tracking in Java

← prev next →