Less CommentsLess comments are non-executable statements that are placed inside the source code. These comments are written to make source code clear and easier to understand by other developers and testers. Comments can be written in block style and inline within the Less code, but single line comments are not appeared in CSS code. There are two types of comments supported in Less.
Less Comment ExampleLet's take an example to demonstrate the sage of comments in Less file. See this example: Create an HTML file named "simple.html", having the following data. HTML file: simple.html Create a LESS file named "simple.less", having the following data. This file also contains single line and multiline comments. LESS file: simple.less Put the both file "simple.html" and "simple.less" inside the root folder of Node.js Now, execute the following code: lessc simple.less simple.css 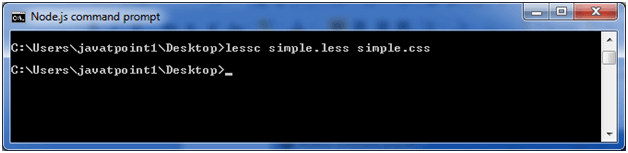
This will compile the "simple.less" file. A CSS file named "simple.css" will be generated. For example: 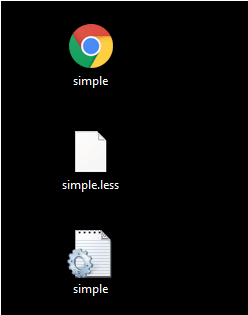
The generated CSS "simple.css", has the following code: Note: In the above code, you can see that only multiline comments are preserved in the generated CSS and single line comments are declined. Output: 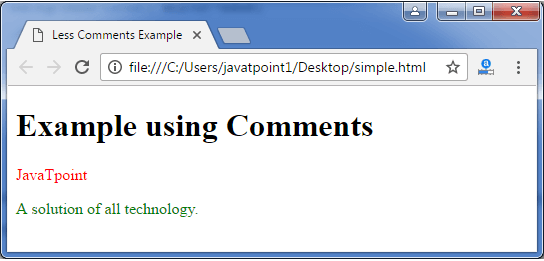
Next TopicLess Syntax
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










