Normal and Trace of a Matrix in Java

In this section, we will learn how to calculate the normal and trace of a matrix in Java. Before moving to, the program, first we will understand the what is normal and trace of a matrix.

Normal of a Matrix

The normal of a matrix is the square root of the sum of squares of all the elements of a matrix. For example, consider the following matrix.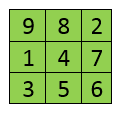

First, we will calculate the sum of the square of each element.

9²+ 8² + 2² + 1² + 4² + 7² + 3² + 5² + 6²

81 + 64 + 4 + 1 + 16 + 49 + 9 + 25 + 36 = 285

Now, calculate the square root of the sum of squares.

√285 = 16.8819430161

Trace of a Matrix

The trace of a matrix is the sum of all the elements present in the principal diagonal (upper left to lower right). Note that the matrix must be a square matrix (the number of rows and columns must be the same). It is useful to prove results in linear algebra. For example, consider the following matrix.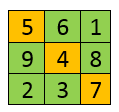

Trace for the above matrix is 5 + 4 + 7 = 16.

Java Program to Find Normal and Trace of a Matrix

MatrixNormalTrace1.java

import 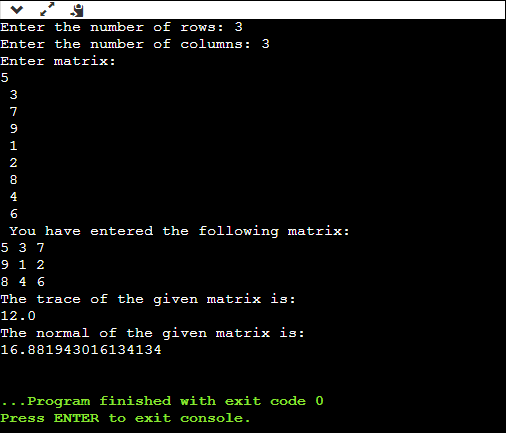java.util.*;
public class MatrixNormalTrace1
{
    public static void main(String args[])
    {
        int array[][] = new int[5][5];
        int i, j;
        double sum = 0, square = 0, result = 0;
  	Scanner s = new Scanner(System.in);
  	System.out.print("Enter the number of rows: ");
  	//reads number of rows from the user
  	int row = s.nextInt();
  	System.out.print("Enter the number of columns: ");
  	//reads number of columns from the user
  	int column = s.nextInt();
	System.out.println("Enter matrix:");
	//loop for rows
 	for(i = 0; i < row; i++)
  	{
  	    //loop for columns
   	    for(j = 0; j < column; j++) 
     	    {
     	        //reads the matrix elements 
      	        array[i][j] = s.nextInt();
      	        //prints space
                System.out.print(" ");
     	    }
        }
	System.out.println("You have entered the following matrix: ");
	//prints the matrix
 	for(i = 0; i < row; i++)
        {
      	    for(j = 0; j < column; j++)
            {
         	System.out.print(array[i][j]+" ");
            }
            System.out.println(" ");
    	}
        System.out.println("The trace of the given matrix is: ");
  	for(i = 0; i < row; i++)
  	{  
    	    for(j = 0; j < column; j++)
       	    {
       	        //checks if an element is of the same rows and column or not, if same calculates trace of the matrix
                if(i == j)
            	 {
            	     //find the sum of principal diagonal
               	     sum = sum + (array[i][j]);
               	 }
            }
        }
        //prints trace
        System.out.println(sum);  
        System.out.println("The normal of the given matrix is: "); 
        
   	for(i = 0; i < row; i++)
   	{
    	    for(j = 0; j < column; j++)
       	    {
       	        //calculates the sum of square of matrix elements 
       	        square = square + (array[i][j])*(array[i][j]);
            }
    	}
    	//calculates square root of the sum
        result = Math.sqrt(square);
        //prints normal of the given matrix
        System.out.println(result);
    }
}

Output:

Similarly, we can also find the normal and trace of a matrix using function.

MatrixNormalTrace2.java

import 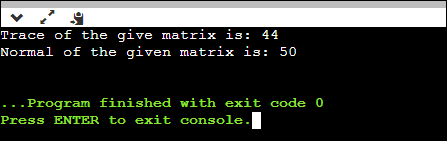java.io.*;
public class MatrixNormalTrace2
{
//size of the given matrix
static int MAX = 10;
//the method calculates and returns Normal of a matrix 
static int calculateNormal(int matrix[][], int n)
{
	int sum = 0;
	for (int i=0; i<n; i++)
		for (int j=0; j<n; j++)
			sum = sum + matrix[i][j]*matrix[i][j];
	return (int)Math.sqrt(sum);
}
//the method calculates and returns trace of a matrix
static int calculateTrace(int matrix[][], int n)
{
	int sum = 0;
	for (int i=0; i<n; i++)
		sum = sum + matrix[i][i];
	return sum;
}
//driver code
public static void main (String args[]) 
    {
        //initializing matrix elements 
		int matrix[][] = {{6, 3, 2, 1, 4},
		                  {7, 8, 3, 12, 9},
		                  {1, 11, 10, 5, 8},
		                  {5, 18, 6, 9, 14},
		                  {19, 23, 3, 12, 11},
	                     };
	    System.out.println ("Trace of the give matrix is: "+ calculateTrace(matrix, 5));
	    System.out.println ("Normal of the given matrix is: "+ calculateNormal(matrix, 5));
	}
}

Output:

Next TopicRight View of a Binary Tree in Java

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

Javatpoint Services

JavaTpoint offers too many high quality services. Mail us on h[email protected], to get more information about given services.

Website Designing
Website Development
Java Development
PHP Development
WordPress
Graphic Designing
Logo
Digital Marketing
On Page and Off Page SEO
PPC
Content Development
Corporate Training
Classroom and Online Training
Data Entry

Training For College Campus

JavaTpoint offers college campus training on Core Java, Advance Java, .Net, Android, Hadoop, PHP, Web Technology and Python. Please mail your requirement at [email protected].
Duration: 1 week to 2 week

^{Like/Subscribe us for latest updates or newsletter}