Pancake Number in Java

In this section, we will discuss what is pancake number and also create Java programs with different approaches to find the pancake number. The pancake number program frequently asked in Java coding interviews and academics.

Pancake Number

A pancake number P_j represents the maximum number of pieces of a circle or pancake that can be divided using j number of cuts. Pancake numbers are also known as lazy caterer numbers, more formally it is known as central polygonal numbers.

Mathematically, the pancake number P_j is represented as: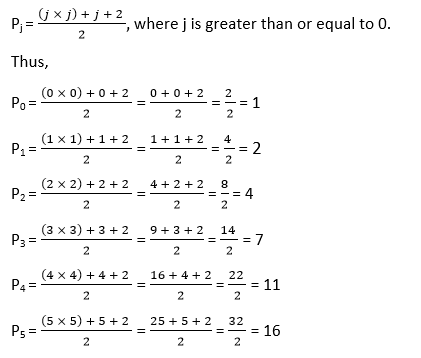

The following diagram shows the pancake numbers for the values j = 0 to j = 5.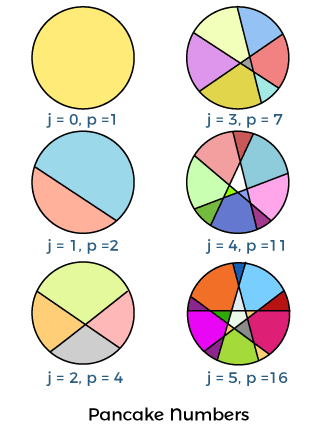

Pancake Number Java Program

The following code shows the implementation of the pancake numbers using the mathematical formula defined above.

FileName: PancakeNumberExample.java

public class PancakeNumberExample  
{

// main method 
public static void main (String argvs[])
{
int n = 10;

// loop for finding and printing
// the first 10 pancake numbers
for(int j = 0; j < n; j++)
{
// using the mathematical formula
int p = ((j * j) + j + 2) / 2;
System.out.print("For j = " + j);
System.out.println(", the pancake number is: " + p);
}

}
}

Output:

For j = 0, the pancake number is: 1
For j = 1, the pancake number is: 2
For j = 2, the pancake number is: 4
For j = 3, the pancake number is: 7
For j = 4, the pancake number is: 11
For j = 5, the pancake number is: 16
For j = 6, the pancake number is: 22
For j = 7, the pancake number is: 29
For j = 8, the pancake number is: 37
For j = 9, the pancake number is: 46

Pancake Number Using Combination

The pancake numbers can also be obtained using combinations. Using combinations, the pancake numbers are defined as:

P_j = ⁰C₀ = 1, for j = 0

P_j = ¹C₀ + ¹C₁ = 1 + 1 = 2, for j = 1

For j >= 2,

P_j = ^jC₀ + ^jC₁ + ^jC₂

Thus,

For j = 2,

P₂ = ²C₀ + ²C₁ + ²C₂ = 1 + 2 + 1 = 4

For j = 3,

P₃ = ³C₀ + ³C₁ + ³C₂ = 1 + 3 + 3 = 7

For j = 4,

P₄ = ⁴C₀ + ⁴C₁ + ⁴C₂ = 1 + 4 + 6 = 11

For j = 5,

P₅ = ⁵C₀ + ⁵C₁ + ⁵C₂ = 1 + 5 + 10 = 16

Combining the above formula for j = 0, 1, and >= 2, we get

P_j = 1, for j = 0, and

P_j = ^{j + 1}C₂ + 1, for j >= 1

Thus,

P₀ = 1

P₁ = ^{1 + 1}C₂ + 1 = ²C₂ + 1 = 1 + 1 = 2

P₂ = ^{2 + 1}C₂ + 1 = ³C₂ + 1 = 3 + 1 = 4

P₃ = ^{3 + 1}C₂ + 1 = ⁴C₂ + 1 = 6 + 1 = 7

Pancake Number: Iterative Approach

Let's implement the above combination formula to compute the pancake numbers.

FileName: PancakeNumberExample1.java

public class PancakeNumberExample1  
{
public int findPancakeNo(int j)
{
// handling the base case
if(j == 0)
{
return 1;
}

int num = 1;

// for calculating (j + 1)!
for(int c = 1; c <= j + 1; c++)
{
num = num * c;
}

int denom = 1;

// for calculating ((j + 1) - 2)!
for(int c = 1; c <= j - 1; c++)
{
denom = denom * c;
}

// caculating (j + 1)!/(((j + 1) - 2)! * 2!) + 1
num = num / denom;
num = num / 2;
num = num + 1;


// returning the computed pancake number
return num;


}

// main method 
public static void main (String argvs[])
{
int n = 10;

// creating an object of the class PancakeNumberExample1
PancakeNumberExample1 obj = new PancakeNumberExample1();


// loop for finding and printing
// the first 10 pancake numbers
for(int j = 0; j < n; j++)
{
// invoking the method findPancakeNo()
int p = obj.findPancakeNo(j);
System.out.print("For j = " + j);
System.out.println(", the pancake number is: " + p);
}

}
}

Output:

For j = 0, the pancake number is: 1
For j = 1, the pancake number is: 2
For j = 2, the pancake number is: 4
For j = 3, the pancake number is: 7
For j = 4, the pancake number is: 11
For j = 5, the pancake number is: 16
For j = 6, the pancake number is: 22
For j = 7, the pancake number is: 29
For j = 8, the pancake number is: 37
For j = 9, the pancake number is: 46

Pancake Number: Recursive Approach

The combination formula can also be implemented using recursion. The following program shows the same.

FileName: PancakeNumberExample2.java

public class PancakeNumberExample2  
{
public int findPancakeNo(int j, int b)
{
// handling the base case
if(j == 0 || b == 0)
{
return 1;
}


// The recursion is based on the nCr = n / r * (n - 1)C(r - 1)
// property of combination
int temp = findPancakeNo(j - 1, b - 1);
temp = (temp * j) / b;
return temp;

}

// main method 
public static void main (String argvs[])
{
int n = 10;

// creating an object of the class PancakeNumberExample2
PancakeNumberExample2 obj = new PancakeNumberExample2();


// loop for finding and printing
// the first 10 pancake numbers
for(int j = 0; j < n; j++)
{
// invoking the method findPancakeNo()
int p;

if(j == 0)
{
// for j = 0, p = 1
p = 1;
}
else
{
p = obj.findPancakeNo(j + 1, 2) + 1;
}

System.out.print("For j = " + j);
System.out.println(", the pancake number is: " + p);
}

}
}

Output:

For j = 0, the pancake number is: 1
For j = 1, the pancake number is: 2
For j = 2, the pancake number is: 4
For j = 3, the pancake number is: 7
For j = 4, the pancake number is: 11
For j = 5, the pancake number is: 16
For j = 6, the pancake number is: 22
For j = 7, the pancake number is: 29
For j = 8, the pancake number is: 37
For j = 9, the pancake number is: 46

Next TopicPancake Sorting in Java

← prev next →