Permutation of Numbers in Java

In this section, we will create a Java program and find the permutation and cyclic permutation of a number. Before moving ahead in this section, first, we will understand permutation with examples.

Permutation

In mathematics, the permutation is a method or technique in which we can determine the possible arrangements in a set. The number of ways of selection and arrangement of items in which orders matters. In short, the permutation is the number of arrangements. While determining the permutation, keep order in mind. It is denoted by the letter P.

In other words, it is a technique by which we can arrange (or select) r objects out of given n objects in a particular order.

Mathematically, we can find the permutation of the numbers by using the following formula: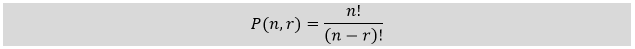

Where,

P: P is the number of permutations.

n: n is the total number of objects in the set.

r: r is the number of choosing objects from the set.

!: The symbol denotes the factorial.

For example, if XYZ is a word then the possible permutations of the word will be:

Hence, we can arrange the word XYZ in six distinct ways.

Let's see an example.

Example: There are six people participating in a skit. In how many ways first and the second prize can be awarded?

Solution:

Given:

n=6, r=2, P=?

According to the above formula: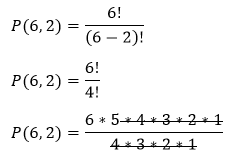

4, 3, 2, 1 are presented in both nominator and denominator so, they are canceled out.

P(6,2)=6*5

P(6,2)=30

Hence, there are 30 possible ways to award the first and second prizes.

Let's implement the above approach in a Java program.

PermutationExample1.java

Output:

Enter the Value of n and r: 
7 4
The permutation of P(n, r) = 840

Let's create another Java program and find the permutation of a number n greater than the number itself.

PermutationExample2.java

Output:

132
213
231
312
321

Using Heap Algorithm

It is an iterative algorithm. By using the heap algorithm, we can find all the permutations of n objects.

• The algorithm generates (n-1)! permutations of the first n-1 elements, adjoining the last element to each of these. This will generate all of the permutations that end with the last element.
• If n is odd, swap the first and last element and if n is even, then swapping the i^th element (i is the counter starting from 0) and the last element and repeat the above algorithm till i is less than n.
• In each iteration, the algorithm will produce all the permutations that end with the current last element.

Let's implement the algorithm in a Java program.

PermutationExample3.java

Output:

8 2 6 7 
2 8 6 7 
6 8 2 7 
8 6 2 7 
2 6 8 7 
6 2 8 7 
7 2 6 8 
2 7 6 8 
6 7 2 8 
7 6 2 8 
2 6 7 8 
6 2 7 8 
7 8 6 2 
8 7 6 2 
6 7 8 2 
7 6 8 2 
8 6 7 2 
6 8 7 2 
7 8 2 6 
8 7 2 6 
2 7 8 6 
7 2 8 6 
8 2 7 6 
2 8 7 6

Using Recursive Algorithm

The recursive algorithm uses backtracking. It demines the permutation of numbers by swapping one element per iteration.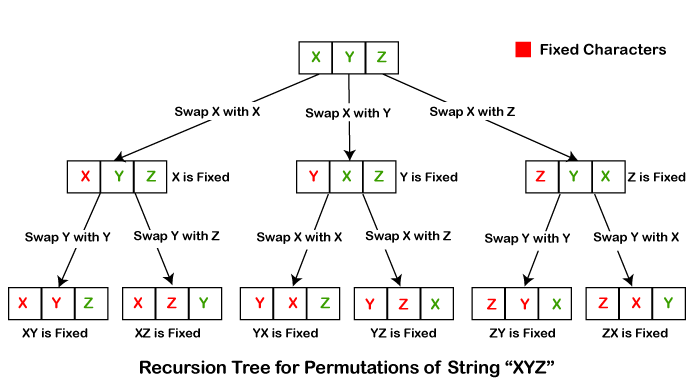

Let's implement the algorithm in a Java program.

PermutationExample4.java

Output:

come
coem
cmoe
cmeo
cemo
ceom
ocme
ocem
omce
omec
oemc
oecm
moce
moec
mcoe
mceo
meco
meoc
eomc
eocm
emoc
emco
ecmo
ecom

Randomized Algorithm

We can also apply the randomized algorithm for determining the permutation of numbers. It is used if the value of n is big. The algorithm generates the permutations by shuffling the array. For shuffling, the Java Collections class provides the shuffle() method.

The shuffle() method randomly permutates the specified List using a default source of randomness. It traverses the list in a backward (from the last element to the second element) direction. It randomly swaps the selected element with the current position. The method runs in linear time. The signature of the method is:

Generating Cyclic Permutations

A permutation composed of a single cycle is known as the cyclic permutation. It shifts all the elements of a set by a fixed offset. The technique can be applied to any integer to shift cyclically right or left by any given number of places. If a set has elements {a, b, c}, then:

• Cyclic permutation one place left generates: {c, a, b}
• Cyclic permutation one place right generates: {a, b, c}

Suppose n is a number whose cyclic permutation is to be found. We can find the cyclic permutation by using the following steps. It generates the next permutation.

We execute the above steps until we get the original number. As soon as, we get the original number, we stop performing the above steps and return the remainder.

For example, find the division of the following fractions:

2/7 = 0.285714...

4/7 = 0.571428...

1/7 = 0.142857...

Let's create a Java program and generate all the possible cyclic permutations.

PermutationExample5.java

Output:

9871
1987
7198
8719