Playfair Cipher Program in Java

Playfair cipher is proposed by Charles Whetstone in 1889. But it was named for one of his friends Lord Lyon Playfair because he popularized its uses. It is the most popular symmetric encryption technique that falls under the substitution cipher. It is an encoding procedure that enciphers more than one letter at a time. In this section, we will discuss Playfair cipher along with its implementation in a Java program.

Playfair Cipher

Playfair cipher is an encryption algorithm to encrypt or encode a message. It is the same as a traditional cipher. The only difference is that it encrypts a digraph (a pair of two letters) instead of a single letter.

It initially creates a key-table of 5*5 matrix. The matrix contains alphabets that act as the key for encryption of the plaintext. Note that any alphabet should not be repeated. Another point to note that there are 26 alphabets and we have only 25 blocks to put a letter inside it. Therefore, one letter is excess so, a letter will be omitted (usually J) from the matrix. Nevertheless, the plaintext contains J, then J is replaced by I. It means treat I and J as the same letter, accordingly.

Since Playfair cipher encrypts the message digraph by digraph. Therefore, the Playfair cipher is an example of a digraph substitution cipher.

Before moving ahead, let's understand the terminology used in this Playfair cipher.

Terminology

• Plaintext: It is the original message that is to be encrypted. It is also known as a message.
• Ciphertext: It is an encrypted message.
• Cipher: It is an algorithm for transforming plaintext to ciphertext.
• Key: It is the key to encrypt or decrypt the plaintext. It is known only to the sender and receiver. It is filled character by character in the matrix that is called key-table or key-matrix.
• Encipher: The process of converting plaintext into ciphertext is called encipher.
• Decipher: The process of removing ciphertext from plaintext is called decipher.
• Cryptanalysis: It is the study of the methods and principles of deciphering ciphertext without knowing the key.

Advantages of Playfair Cipher

1. Diverse ciphertext if we scrutinize the Algorithm, we can notice at every Stage we are getting diverse ciphertext, thus more trouble to cryptanalyst.
2. Brute force attack does not affect it.
3. Cryptanalyze (the process of decoding cipher without knowing key) is not possible.
4. Overcomes the limitation of simple Playfair square cipher.
5. Easy to perform the substitution.

Limitations of Playfair Cipher

The limitations of the Playfair cipher are as follows:

• Only 25 alphabets are supported.
• It does not support numeric characters.
• Only either upper cases or lower cases are supported.
• The use of special characters (such as blank space, newline, punctuations, etc.) is prohibited.
• It does not support other languages, except English.
• Encryption of media files is also not supported.

Playfair Cipher Encryption Rules

1. First, split the plaintext into digraphs (pair of two letters). If the plaintext has the odd number of letters, append the letter Z at the end of the plaintext. It makes the plaintext of even For example, the plaintext MANGO has five letters. So, it is not possible to make a digraph. Since, we will append a letter Z at the end of the plaintext, i.e. MANGOZ.

2. After that, break the plaintext into digraphs (pair of two letters). If any letter appears twice (side by side), put X at the place of the second occurrence. Suppose, the plaintext is COMMUNICATE then its digraph becomes CO MX MU NI CA TE. Similarly, the digraph for the plaintext JAZZ will be JA ZX ZX, and for plaintext GREET, the digraph will be GR EX ET.

3. To determine the cipher (encryption) text, first, build a 5*5 key-matrix or key-table and filled it with the letters of alphabets, as directed below:

• Fill the first row (left to right) with the letters of the given keyword (ATHENS). If the keyword has duplicate letters (if any) avoid them. It means a letter will be considered only once. After that, fill the remaining letters in alphabetical order. Let's create a 5*5 key-matrix for the keyword ATHENS.

Note that in the above matrix any letter is not repeated. The letters in the first row (in green color) represent the keyword and the remaining letters sets in alphabetical order.

4. There may be the following three conditions:

i) If a pair of letters (digraph) appears in the same row

In this case, replace each letter of the digraph with the letters immediately to their right. If there is no letter to the right, consider the first letter of the same row as the right letter. Suppose, Z is a letter whose right letter is required, in such case, T will be right to Z.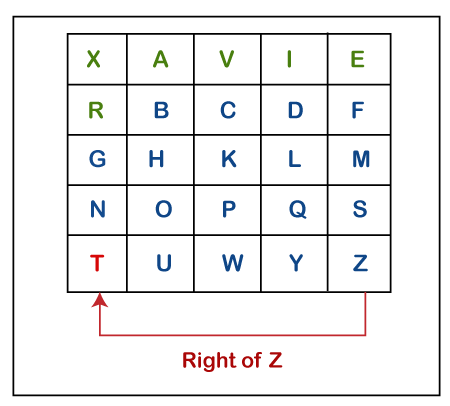

ii) If a pair of letters (digraph) appears in the same column

In this case, replace each letter of the digraph with the letters immediately below them. If there is no letter below, wrap around to the top of the same column. Suppose, W is a letter whose below letter is required, in such case, V will be below W.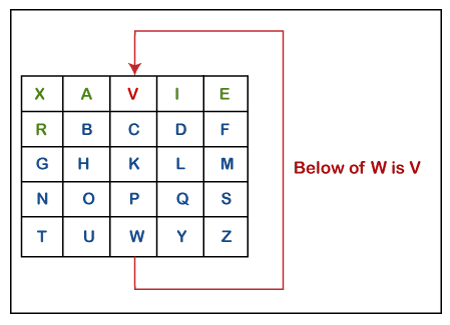

iii) If a pair of letters (digraph) appears in a different row and different column

In this case, select a 3*3 matrix from a 5*5 matrix such that pair of letters appear in the 3*3 matrix. Since they occupy two opposite corners of a square within the matrix. The other corner will be a cipher for the given digraph.

In other words, we can also say that intersection of H and Y will be the cipher for the first letter and

Suppose, a digraph is HY and we have to find a cipher for it. We observe that both H and Y are placed in different rows and different columns. In such cases, we have to select a 3*3 matrix in such a way that both H and Y appear in the 3*3 matrix (highlighted with yellow color). Now, we will consider only the selected matrix to find the cipher.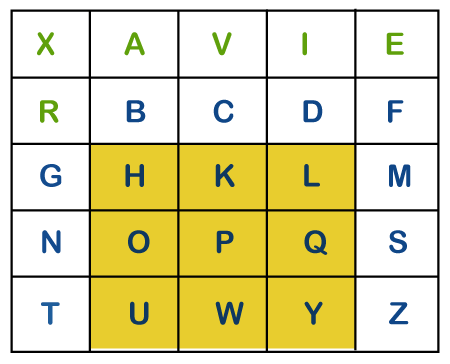

Now to find the cipher for HY, we will consider the diagonal opposite to HY, i.e. LU. Therefore, the cipher for H will be L, and the cipher for Y will be U.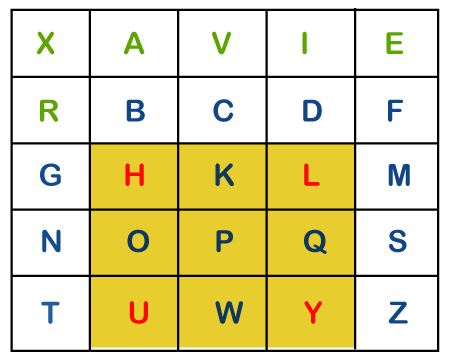

Note: The order of the letters within the digraph is not important.

Playfair Cipher Decryption

The decryption procedure is the same as encryption but the steps are applied in reverse order. For decryption cipher is symmetric (move left along rows and up along columns). The receiver of the plain text has the same key and can create the same key-table that is used to decrypt the message.

Let's see an example of Playfair cipher.

Example of Playfair Cipher

Suppose, the plaintext is COMMUNICATION and the key that we will use to encipher the plaintext is COMPUTER. The key can be any word or phrase. Let's encipher the message COMMUNICATION.

1. First, split the plaintext into digraph (by rule 2) i.e. CO MX MU NI CA TE.

2. Construct a 5*5 key-matrix (by rule 3). In our case, the key is COMPUTER.

3. Now, we will traverse in key-matrix pair by pair and find the corresponding encipher for the pair.

• The first digraph is CO. The pair appears in the same row. By using Rule 4(i) CO gets encipher into OM.
• The second digraph is MX. The pair appears in the same column. By using Rule 4(ii) MX gets encipher into RM.
• The third digraph is MU. The pair appears in the same row. By using Rule 4(i) MU gets encipher into PC.
• The fourth digraph is NI. The pair appears in different rows and different columns. By using Rule 4(iii) NI gets encipher into SG.
• The fifth digraph is CA. The pair appears in different rows and different columns. By using Rule 4(iii) CA gets encipher into PT.
• The sixth digraph is TE. The pair appears in the same row. By using Rule 4(i) TE gets encipher into ER.

Therefore, the plaintext COMMUNICATE gets encipher (encrypted) into OMRMPCSGPTER.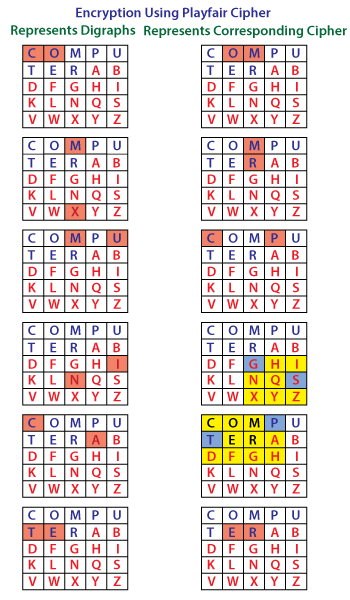

Let's implement the above logic in a Java program.

Playfair Java Program

PlayfairCipher.java

Output 1:

Output 2: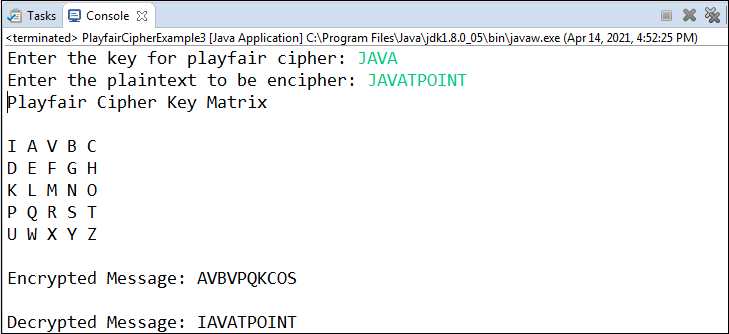

Output 3: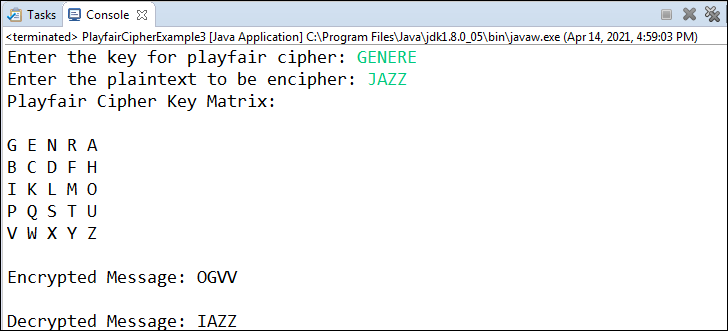

In comparison to monoalphabetic cipher, the Playfair cipher (polyalphabetic cipher) is more secure. Because in monoalphabetic cipher the attacker has to search only in 26 letters. While in polyalphabetic cipher attacker has to search for 26² (676) digraphs. An attacker can still break the cipher in monoalphabetic cipher. Although frequency analysis is much more difficult and it uses modern computational techniques. Therefore, performing double substitution and transposition on Playfair cipher substantially increases its security.