Star Numbers in Java

In this section, we are going to learn about stars numbers in Java. The stars number resembles the board of the Chinese checkers game. A star number is a hexagram. Here, a hexagram means a six-pointed star. Observe the following diagram.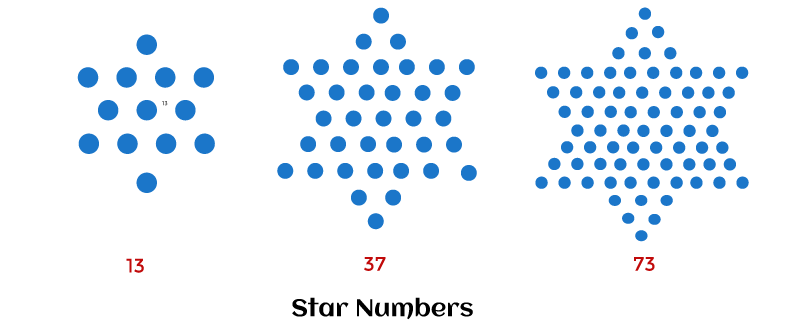

Mathematically, the number is represented by

S_n = 6 x n x (n - 1) + 1, where n >= 1

Thus,

S₁ = 6 x 1 x (1 - 1) + 1 = 6 x 1 x 0 + 1 = 0 + 1 = 1

S₂ = 6 x 2 x (2 - 1) + 1 = 6 x 2 x 1 + 1 = 12 + 1 = 13

S₃ = 6 x 3 x (3 - 1) + 1 = 6 x 3 x 2 + 1 = 36 + 1 = 37

S₄ = 6 x 4 x (4 - 1) + 1 = 6 x 4 x 3 + 1 = 72 + 1 = 73

S₅ = 6 x 5 x (5 - 1) + 1 = 6 x 5 x 4 + 1 = 120 + 1 = 121

S₆ = 6 x 6 x (6 - 1) + 1 = 6 x 6 x 5 + 1 = 180 + 1 = 181

Implementation

There are three ways to write the code for the star numbers in Java. One way is using the formula defined above, the other is recursive, and the last one is iterative. Let's start with the formula-based approach.

Formula based Approach

FileName: StarNumbers.java

public class StarNumbers
{

// a method for computing the ith star number
public int findStarNumbers(int i)
{
    // computing star number using the mathematical formula 
    // defined above
    int starNum = 6 * i * ( i - 1) + 1;
    
    return starNum;
}


// main method
public static void main(String argvs[])
{
// total number of star numbers that have to be computed
int num = 10;

// creating an object of the class StarNumbers
StarNumbers obj = new StarNumbers();

System.out.println("The first 10 star numbers are: ");
for(int i = 1; i <= num; i++)
{
// invoking the method findStarNumbers() 
// and storing the result
int ans = obj.findStarNumbers(i);
System.out.print(ans + " ");
}


}
}

Output:

The first 10 star numbers are: 
1 13 37 73 121 181 253 337 433 541

Time-Complexity: The time-complexity of the above program is O(n), where n is the total number of star numbers that have to be found.

Space Complexity: The above program is not using any extra space; therefore, the space complexity of the above program is O(1).

Recursive Approach

Using recursion also, one can compute the star numbers. However, before implementing the recursion, one must know the recursive formula for computing the star numbers. The recursive formula is defined as:

S_n = S_{n - 1} + 12 x (n - 1), where n >= 2 and S₁ = 1

Thus,

S₂ = S_{2 - 1} + 12 x (2 - 1) = = S₁ + 12 x 1 = 1 + 12 = 13

S₃ = S_{3 - 1} + 12 x (3 - 1) = = S₂ + 12 x 2 = 13 + 24 = 37

S₄ = S_{4 - 1} + 12 x (4 - 1) = = S₃ + 12 x 3 = 37 + 36 = 73

S₅ = S_{5 - 1} + 12 x (5 - 1) = = S₄ + 12 x 4 = 73 + 48 = 121

S₆ = S_{6 - 1} + 12 x (6 - 1) = = S₅ + 12 x 5 = 121 + 60 = 181

Observe the following Java code.

FileName: StarNumbers1.java

public class StarNumbers1
{

// a method for computing the ith star number recursively
public int findStarNumbers(int i)
{
    // handling the base case S1 = 1
    if(i == 1)
    {
        
        return 1;
    }
    
    else
    {
        // recursively finding the ith star number
        return (findStarNumbers(i - 1) + 12 * (i - 1));    
    }
}


// main method
public static void main(String argvs[])
{
// total number of star numbers that have to be computed
int num = 10;

// creating an object of the class StarNumbers1
StarNumbers1 obj = new StarNumbers1();

System.out.println("The first 10 star numbers are: ");
for(int i = 1; i <= num; i++)
{
// invoking the method findStarNumbers() 
// and storing the result
int ans = obj.findStarNumbers(i);
System.out.print(ans + " ");
}
}
}

Output:

The first 10 star numbers are: 
1 13 37 73 121 181 253 337 433 541

Time-Complexity: For finding the nth star number, one has to recursive go from n to 1. Therefore, the time complexity of the above program is O(n²), where n is the total number of star numbers that have to be computed.

Space Complexity: If we ignore the implicit memory consumption due to recursion, the space complexity of the above program is O(1).

In order to optimize the above program, one has to use the memorization technique. The following program shows the same.

FileName: StarNumbers2.java

public class StarNumbers2
{

// a method for computing the ith star number recursively
public int findStarNumbers(int i, int arr[])
{
    // handling the base case S1 = 1
    if(i == 1)
    {
        
        arr[i] = 1;
        return 1;
    }
    
    // memoization technique is used here
    // For example: for computing the 3rd star number
    // earlier, one has to go recursively from 3 to 1.
    // Therefore, it leads to repetition of computing the 2nd star number
    // In this case, we have already stored the value of 2nd star number
    // in the element arr[2]. All we have to do is to return it
    if(arr[i] != 0)
    {
        return arr[i];
    }
    
    else
    {
        // recursively finding the ith star number
        arr[i] = (findStarNumbers(i - 1, arr) + 12 * (i - 1));  
        return arr[i];
    }
}


// main method
public static void main(String argvs[])
{
// total number of star numbers that have to be computed
int num = 10;

// creating an object of the class StarNumbers2
StarNumbers2 obj = new StarNumbers2();

// for storing the ith star number
int []arr = new int[num];

System.out.println("The first 10 star numbers are: ");
for(int i = 1; i <= num; i++)
{
// invoking the method findStarNumbers() 
// and storing the result
int ans = obj.findStarNumbers(i, arr);
System.out.print(ans + " ");
}


}
}

Output:

The first 10 star numbers are: 
1 13 37 73 121 181 253 337 433 541

Time Complexity: Because of the memorization technique, the time complexity of the above program is O(n), where n is the total number of star numbers that have to be computed.

Space Complexity: The space complexity of the above program is O(n), where n is the total number of star numbers that have to be computed.

Iterative Approach

Using a loop also, one can easily compute the value of the star numbers. The following program shows the same.

FileName: StarNumbers3.java

public class StarNumbers3
{

// a method for computing the ith star number iteratively
public int findStarNumbers(int i)
{
    // an integer array for storing the star numbers
    int []arr = new int[i + 1];
    
    for(int j = 1; j <= i; j++)
    {
        // handling the base case S1 = 1
        if(j == 1)
        {
            arr[j] = 1;
        }
        
        // else part handles the other cases
        else
        {
            arr[j] = arr[j - 1] + 12 * (j - 1);
        }
    }
    
    return arr[i];
}


// main method
public static void main(String argvs[])
{
// total number of star numbers that have to be computed
int num = 10;

// creating an object of the class StarNumbers3
StarNumbers3 obj = new StarNumbers3();

System.out.println("The first " + num + " star numbers are: ");
for(int i = 1; i <= num; i++)
{
// invoking the method findStarNumbers() 
// and storing the result
int ans = obj.findStarNumbers(i);
System.out.print(ans + " ");
}
}
}

Output:

The first 10 star numbers are: 
1 13 37 73 121 181 253 337 433 541

Time Complexity: Because of the for-loop used in the calculation of finding each star number, the time complexity of the above program is O(n²), where n is the total number of star numbers one has to find.

Space Complexity: The space complexity of the above program is O(n), where n is the total number of star numbers that have to be computed.

We can optimize the above code to reduce the time complexity. See the following program.

FileName: StarNumbers4.java

public class StarNumbers4
{

// main method
public static void main(String argvs[])
{
// total number of star numbers that have to be computed
int num = 10;


// an integer array for storing the star numbers
int []arr = new int[num + 1];


System.out.println("The first " + num + " star numbers are: ");
for(int i = 1; i <= num; i++)
{
// handling the base case S1 = 1
if(i == 1)
{
arr[i] = 1;    
}

// handling the other cases
else
{
arr[i] = arr[i - 1] + 12 * (i - 1);
}
System.out.print(arr[i] + " ");
}


}
}

Output:

The first 10 star numbers are: 
1 13 37 73 121 181 253 337 433 541

Time Complexity: As there is only one loop for computing the star numbers; therefore, the time complexity of the above program is O(n), where n is the total number of star numbers one has to find.

Space Complexity: The space complexity of the above program is O(n), where n is the total number of star numbers that have to be computed.

We can still do some optimization to reduce the space complexity of the program. If we observe the recursive formula, we find that the nth star number is dependent on the (n- -1)th star number, and (n - 1)th star number is dependent on the (n - 2)th star number, and so on. That means the current star number is dependent on the previous star number. Therefore, we do not need an array for storing the star numbers. All we have to do is to store the previous star number in a variable to compute the current star number. The following program shows the same.

FileName: StarNumbers5.java

public class StarNumbers5
{

// main method
public static void main(String argvs[])
{
// total number of star numbers that have to be computed
int num = 10;

// for containing the last computed star number
int prv =0;

// for storing the current star number
int curr = 0;

System.out.println("The first " + num + " star numbers are: ");
for(int i = 1; i <= num; i++)
{
// handling the base case S1 = 1
if(i == 1)
{
prv = 1;
curr = 1;
}

// handling the other cases
else
{
// computing the current star number using the previously
// computed star number
curr = prv + 12 * (i - 1);
prv = curr;
}
System.out.print(curr + " ");
}


}
}

Output:

The first 10 star numbers are: 
1 13 37 73 121 181 253 337 433 541

Space Complexity: As we are using only two variables for computing the star numbers; therefore, the space complexity of the above program is O(1).

Relation with the Other Numbers

There are many star numbers that are also triangular numbers. Numbers such as 1, 253, 49141, and many more are the star as well as the triangular number.
There are many star numbers that are also square numbers. Numbers such as 1 = 1², 121 = 11², 11881 = 109², and many more are the star as well as the square number.
A star prime number is a number that is a prime as well as a star number. For example: 13, 37, 73, and many more are the star as well as the prime numbers.

Next Topic3N+1 Problem in Java

← prev next →