Strobogrammatic Number in Java

In this section, we will learn what is a strobogrammatic numbers and also create Java programs to check if the given number is a strobogrammatic numbers or not. The strobogrammatic numbers Java program is frequently asked in Java coding interviews and academics.

Strobogrammatic numbers, an interesting mathematical concept, exhibit a unique quality: rotated 180 degrees, they look the same. In a nutshell, they read the same thing intentionally, such as the letters 0, 1, 8, 11, 69. Analysing and understanding these numbers not only explores mathematical questions but provides procedural challenges which is also interesting.

Strobogrammatic Numbers

Strobogrammatic numbers are numerical palindromes that do not change under rotation. They are symmetrical and have reflexive properties. For example, the number 69 remains the same and becomes 96 after turning 180 degrees. It is defined in OEIS sequence A000787, whereas strobogrammatic prime numbers are defined in OEIS sequence A007597.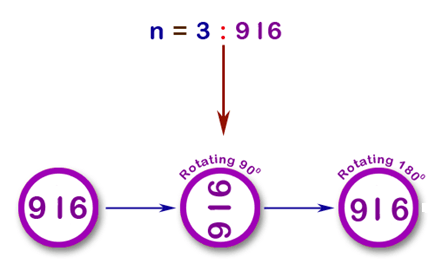

Strobogrammatic Numbers Example

The first few strobogrammatic numbers are: 0, 1, 8, 11, 69, 88, 96, 101, 111, 181, 609, 619, 689, 808, 818, 888, 906, 916, 986, 1001, 1111, 1691, 1881, 1961, 6009, 6119, 6699, 6889, 6969, 8008, 8118, 8698, 8888, 8968, 9006, 9116, 9696, 9886, 9966, …

Finding Strobogrammatic Numbers

The approach for finding the strobogrammatic number is, first, we determine what each digit become when we rotate it by 180 degrees. There are three possibilities for each digit.

Either digit becomes invalid, remains the same, becomes a different digit.

Consider a digit to be rotate by 180 degrees if and only if it becomes a valid digit. If we look at numbers we see that the numbers 0, 1, 6, 8, 9 are rotatable as these are valid digits. So if the number contains any digit other than these, we can say that it is not a strobogrammatic number. For other digits, we need to check if their rotation is the same as the number at its counterpart.

Let's implement the above approach in a Java program.

Strobogrammatic Numbers Java Program

In Java, we explore how to learn strobogrammatic numbers systematically. One way is to list all possible strobogram numbers in the space provided and check if each number belongs to this set.

File Name: StrobogrammaticNumbers.java

import java.util.*; public class StrobogrammaticNumbers { public static List<String> findStrobogrammatic(int n) { return findStrobogrammaticHelper(n, n); } public static List<String> findStrobogrammaticHelper(int n, int m) { if (n == 0) return new ArrayList<>(Arrays.asList("")); if (n == 1) return new ArrayList<>(Arrays.asList("0", "1", "8")); List<String> result = new ArrayList<>(); List<String> center = findStrobogrammaticHelper(n - 2, m); for (String s : center) { if (n != m) result.add("0" + s + "0"); result.add("1" + s + "1"); result.add("6" + s + "9"); result.add("8" + s + "8"); result.add("9" + s + "6"); } return result; } public static void main(String[] args) { int n = 3; // Change n to the desired length of strobogrammatic numbers List<String> strobogrammaticNumbers = findStrobogrammatic(n); System.out.println("Strobogrammatic numbers of length " + n + ": " + strobogrammaticNumbers); } }

Output:

Strobogrammatic numbers of length 3: [101, 609, 808, 906, 111, 619, 818, 916, 181, 689, 888, 986]

Explanation

The findStrobogrammatic() method produces all strobogrammatic numbers of length n.

The findStrobogrammaticHelper() method typically returns strobogrammatic numbers.

We repeat over the middle digits and add two reflexive digits to create strobogrammatic numbers.

Complexity

Time Complexity: O(n)

Space Complexity: O(1)

Conclusion

Strobogrammatic numbers, with their interesting properties, provide fascinating insights into both mathematics and organization. In Java, we can use recursive methods to find and optimize these numbers. Adding strobogrammatic numbers to our programming arsenal not only enhances our problem solving skills but also adds a little mathematical elegance to our code. Explore further, try different techniques, and embrace the beauty of strobogrammatic numbers in your Java projects.

Next Topic5 Types of Java

← prev next →