Travelling Salesman Problem in JavaIn Java, Travelling Salesman Problem is a problem in which we need to find the shortest route that covers each city exactly once and returns to the starting point. Hamiltonian Cycle is another problem in Java that is mostly similar to Travelling Salesman Problem. The main difference between TSP and the Hamiltonian cycle is that in Hamiltonian Cycle, we are not sure whether a tour that visits each city exactly once exists or not, and we have to determine it. In the Travelling Salesman Problem, a Hamiltonian cycle is always present because the graph is complete, and the problem is to find a Hamiltonian cycle with minimum weight. Let's take an example of the Travelling Salesman Problem to understand the problem. 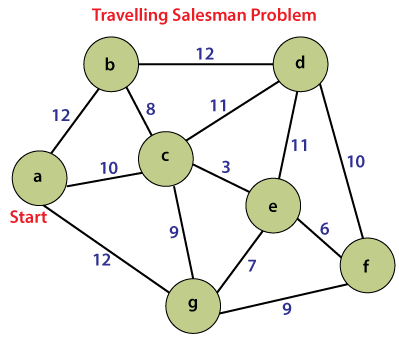
In the above graph, a, b, c, d, e, f, and g are the cities and we have to find the Hamiltonian cycle having minimum weight. There are several Hamiltonian Cycle and some of them are as follows:
The weight of each Hamiltonian cycle can be different, and now our task is to find that route having a minimum distance. Steps to implement Travelling Salesman ProblemThese are the following steps, which we use to implement the TSP program in Java:
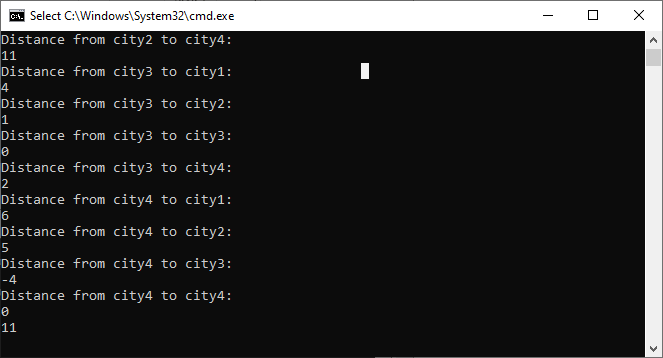
Let's implement the Java code of TSP by using the above steps: TSPExample.java Output 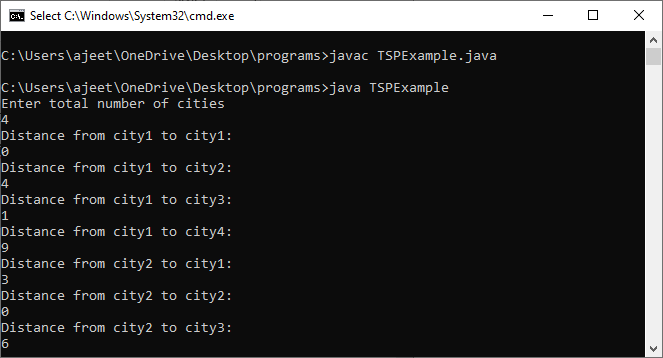
Next TopicDifference Between & and && in Java
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









