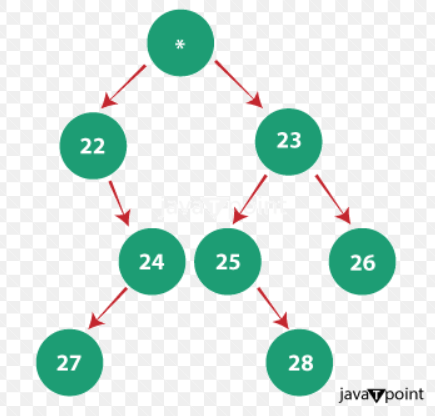
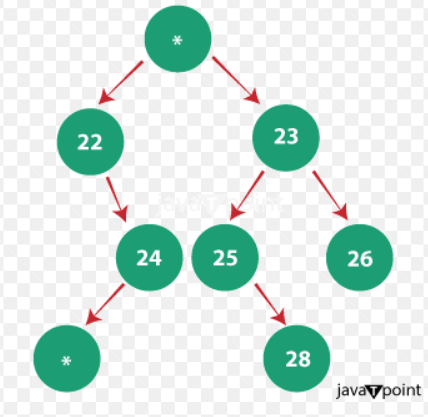
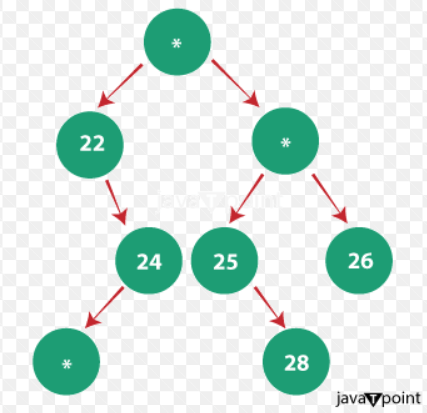
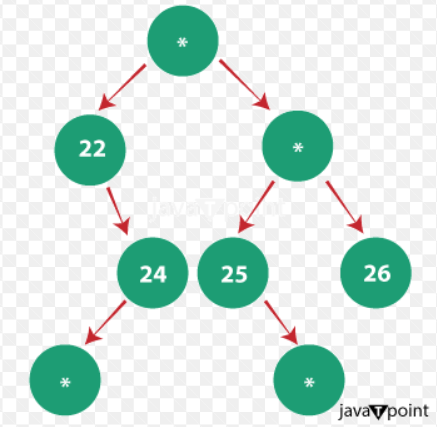
Vertical zig-zag traversal of a tree in Java

The goal is to get the outcome of the items in the Vertical Zig-Zag traversal order given a Binary Tree. A tree's vertical zigzag traversal is described as follows:

1. List the first level's elements in the correct order from right to left; if no parts remain, move on to the next level.
2. If there are no more elements in the last level, print them from left to right. If not, move on to the level before.
3. While there are still nodes to navigate, follow the previous instructions.

Example 1:

Input: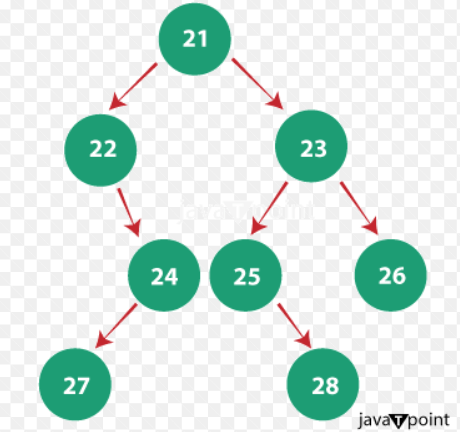

Output:

The order of elements after traversing is:

21, 27, 23, 28, 22, 24, 26, 25

Explanation:

1. The First step is to print elements for the first level will be printed as follows: 1.
2. Currently, the remaining tree portion is given by
   
3. Proceed to the fourth level print from the element that is farthest to the left, which is: 7.
4. Now the tree transforms into:
   
5. Now, as we are moving from the second level to the higher level, we should start at the rightmost position, making the element: 3.
6. Now the tree transforms into:
   
7. Proceed once more to the fourth level print from the last element on the left, which is element 8.
8. Now the tree transforms into:
   
9. Return to level 2 print now, starting with the element that is farthest to the right, which is 2. do thus until none of the elements have been traversed.

Algorithm

Step 1: Make a vector tree[] in which all of the tree's nodes at level i will be stored in tree[i].

Step 2: Take two pointers, p1 and p2, respectively, pointing to the first and last levels.

Step 3: Now, use these two pointers to begin printing the nodes alternately (from left to right for p2 and from right to left for p1).

Step 4: Proceed to the next level if there are no more nodes in the level that p1 points to, and back to the previous level if there are no more nodes in the level that p2 points to.

Implementation:

FileName: VerticalZigZag.java

Output:

The order after traversing: 
21 27 23 28 22 24 26 25

Complexity Analysis:

The time complexity is O(n) and the space complexity is O(n).