Arden's TheoremThe Arden's Theorem is useful for checking the equivalence of two regular expressions as well as in the conversion of DFA to a regular expression. Let us see its use in the conversion of DFA to a regular expression. Following algorithm is used to build the regular expression form given DFA. 1. Let q1 be the initial state. 2. There are q2, q3, q4 ....qn number of states. The final state may be some qj where j<= n. 3. Let αji represents the transition from qj to qi. 4. Calculate qi such that qi = αji * qj If qj is a start state then we have: qi = αji * qj + ε 5. Similarly, compute the final state which ultimately gives the regular expression 'r'. Example:Construct the regular expression for the given DFA 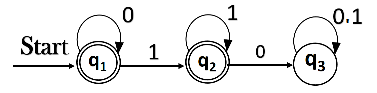 Solution: Let us write down the equations q1 = q1 0 + ε Since q1 is the start state, so ε will be added, and the input 0 is coming to q1 from q1 hence we write Similarly, q2 = q1 1 + q2 1 q3 = q2 0 + q3 (0+1) Since the final states are q1 and q2, we are interested in solving q1 and q2 only. Let us see q1 first q1 = q1 0 + ε We can re-write it as q1 = ε + q1 0 Which is similar to R = Q + RP, and gets reduced to R = OP*. Assuming R = q1, Q = ε, P = 0 We get q1 = ε.(0)* q1 = 0* (ε.R*= R*) Substituting the value into q2, we will get q2 = 0* 1 + q2 1 q2 = 0* 1 (1)* (R = Q + RP → Q P*) The regular expression is given by r = q1 + q2 = 0* + 0* 1.1* r = 0* + 0* 1+ (1.1* = 1+)
Next TopicMoore Machine
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










