Transition Diagram

A transition diagram or state transition diagram is a directed graph which can be constructed as follows:

• There is a node for each state in Q, which is represented by the circle.
• There is a directed edge from node q to node p labeled a if δ(q, a) = p.
• In the start state, there is an arrow with no source.
• Accepting states or final states are indicating by a double circle.

Some Notations that are used in the transition diagram: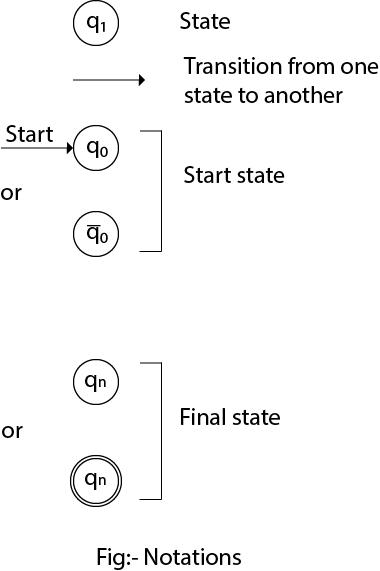

There is a description of how a DFA operates:

1. In DFA, the input to the automata can be any string. Now, put a pointer to the start state q and read the input string w from left to right and move the pointer according to the transition function, δ. We can read one symbol at a time. If the next symbol of string w is a and the pointer is on state p, move the pointer to δ(p, a). When the end of the input string w is encountered, then the pointer is on some state F.

2. The string w is said to be accepted by the DFA if r ∈ F that means the input string w is processed successfully and the automata reached its final state. The string is said to be rejected by DFA if r ∉ F.

Example 1:

DFA with ∑ = {0, 1} accepts all strings starting with 1.

Solution: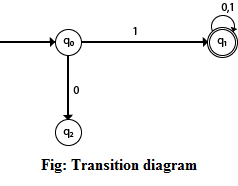

The finite automata can be represented using a transition graph. In the above diagram, the machine initially is in start state q0 then on receiving input 1 the machine changes its state to q1. From q0 on receiving 0, the machine changes its state to q2, which is the dead state. From q1 on receiving input 0, 1 the machine changes its state to q1, which is the final state. The possible input strings that can be generated are 10, 11, 110, 101, 111......., that means all string starts with 1.

Example 2:

NFA with ∑ = {0, 1} accepts all strings starting with 1.

Solution: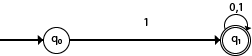

The NFA can be represented using a transition graph. In the above diagram, the machine initially is in start state q0 then on receiving input 1 the machine changes its state to q1. From q1 on receiving input 0, 1 the machine changes its state to q1. The possible input string that can be generated is 10, 11, 110, 101, 111......, that means all string starts with 1.