Introduction to UndecidabilityIn the theory of computation, we often come across such problems that are answered either 'yes' or 'no'. The class of problems which can be answered as 'yes' are called solvable or decidable. Otherwise, the class of problems is said to be unsolvable or undecidable. Undecidability of Universal Languages:The universal language Lu is a recursively enumerable language and we have to prove that it is undecidable (non-recursive). Theorem: Lu is RE but not recursive. Proof: Consider that language Lu is recursively enumerable language. We will assume that Lu is recursive. Then the complement of Lu that is L`u is also recursive. However, if we have a TM M to accept L`u then we can construct a TM Ld. But Ld the diagonalization language is not RE. Thus our assumption that Lu is recursive is wrong (not RE means not recursive). Hence we can say that Lu is RE but not recursive. The construction of M for Ld is as shown in the following diagram: 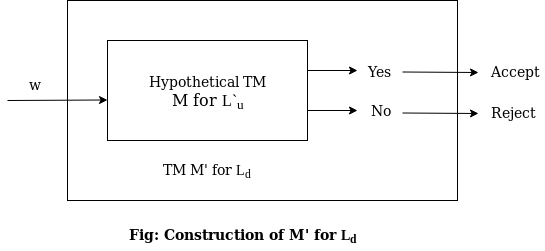
Next TopicUndecidable Problem about TM
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









