Examples of DFAExample 1:Design a FA with ∑ = {0, 1} accepts those string which starts with 1 and ends with 0. Solution: The FA will have a start state q0 from which only the edge with input 1 will go to the next state.  In state q1, if we read 1, we will be in state q1, but if we read 0 at state q1, we will reach to state q2 which is the final state. In state q2, if we read either 0 or 1, we will go to q2 state or q1 state respectively. Note that if the input ends with 0, it will be in the final state. Example 2:Design a FA with ∑ = {0, 1} accepts the only input 101. Solution:  In the given solution, we can see that only input 101 will be accepted. Hence, for input 101, there is no other path shown for other input. Example 3:Design FA with ∑ = {0, 1} accepts even number of 0's and even number of 1's. Solution: This FA will consider four different stages for input 0 and input 1. The stages could be: 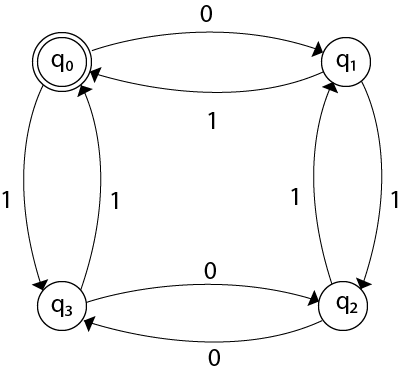 Here q0 is a start state and the final state also. Note carefully that a symmetry of 0's and 1's is maintained. We can associate meanings to each state as: q0: state of even number of 0's and even number of 1's. Example 4:Design FA with ∑ = {0, 1} accepts the set of all strings with three consecutive 0's. Solution: The strings that will be generated for this particular languages are 000, 0001, 1000, 10001, .... in which 0 always appears in a clump of 3. The transition graph is as follows: 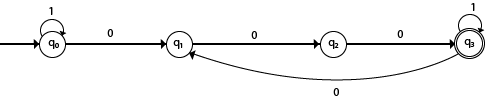 Note that the sequence of triple zeros is maintained to reach the final state.Example 5:Design a DFA L(M) = {w | w ε {0, 1}*} and W is a string that does not contain consecutive 1's. Solution: When three consecutive 1's occur the DFA will be: 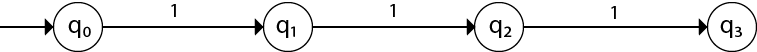 Here two consecutive 1's or single 1 is acceptable, hence  The stages q0, q1, q2 are the final states. The DFA will generate the strings that do not contain consecutive 1's like 10, 110, 101,..... etc. Example 6:Design a FA with ∑ = {0, 1} accepts the strings with an even number of 0's followed by single 1. Solution: The DFA can be shown by a transition diagram as: 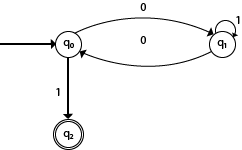
Next TopicNFA
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










