Turing MachineTuring machine was invented in 1936 by Alan Turing. It is an accepting device which accepts Recursive Enumerable Language generated by type 0 grammar. There are various features of the Turing machine:
Formal definition of Turing machineA Turing machine can be defined as a collection of 7 components: Q: the finite set of states The mapping function shows the mapping from states of finite automata and input symbol on the tape to the next states, external symbols and the direction for moving the tape head. This is known as a triple or a program for turing machine. That means in q0 state, if we read symbol 'a' then it will go to state q1, replaced a by X and move ahead right(R stands for right). Example:Construct TM for the language L ={0n1n} where n>=1. Solution: We have already solved this problem by PDA. In PDA, we have a stack to remember the previous symbol. The main advantage of the Turing machine is we have a tape head which can be moved forward or backward, and the input tape can be scanned. The simple logic which we will apply is read out each '0' mark it by A and then move ahead along with the input tape and find out 1 convert it to B. Now, repeat this process for all a's and b's. Now we will see how this turing machine work for 0011. The simulation for 0011 can be shown as below: Now, we will see how this turing machine will works for 0011. Initially, state is q0 and head points to 0 as: 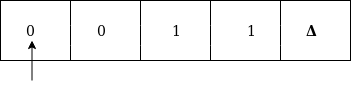 The move will be δ(q0, 0) = δ(q1, A, R) which means it will go to state q1, replaced 0 by A and head will move to the right as:  The move will be δ(q1, 0) = δ(q1, 0, R) which means it will not change any symbol, remain in the same state and move to the right as: 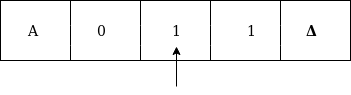 The move will be δ(q1, 1) = δ(q2, B, L) which means it will go to state q2, replaced 1 by B and head will move to left as: 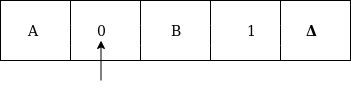 Now move will be δ(q2, 0) = δ(q2, 0, L) which means it will not change any symbol, remain in the same state and move to left as: 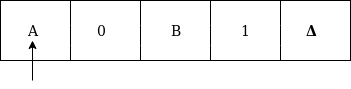 The move will be δ(q2, A) = δ(q0, A, R), it means will go to state q0, replaced A by A and head will move to the right as: 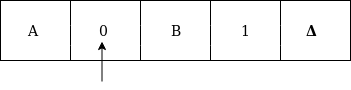 The move will be δ(q0, 0) = δ(q1, A, R) which means it will go to state q1, replaced 0 by A, and head will move to right as: 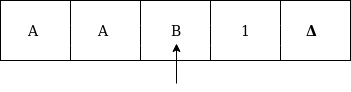 The move will be δ(q1, B) = δ(q1, B, R) which means it will not change any symbol, remain in the same state and move to right as: 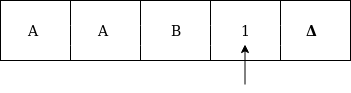 The move will be δ(q1, 1) = δ(q2, B, L) which means it will go to state q2, replaced 1 by B and head will move to left as: 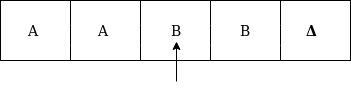 The move δ(q2, B) = (q2, B, L) which means it will not change any symbol, remain in the same state and move to left as: 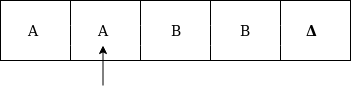 Now immediately before B is A that means all the 0?s are market by A. So we will move right to ensure that no 1 is present. The move will be δ(q2, A) = (q0, A, R) which means it will go to state q0, will not change any symbol, and move to right as: 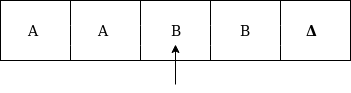 The move δ(q0, B) = (q3, B, R) which means it will go to state q3, will not change any symbol, and move to right as: 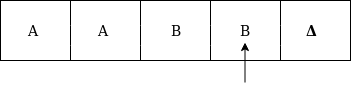 The move δ(q3, B) = (q3, B, R) which means it will not change any symbol, remain in the same state and move to right as: 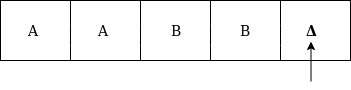 The move δ(q3, Δ) = (q4, Δ, R) which means it will go to state q4 which is the HALT state and HALT state is always an accept state for any TM. 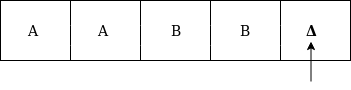 The same TM can be represented by Transition Diagram:
Next TopicBasic Model of Turing machine
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









