Pushdown Automata(PDA)
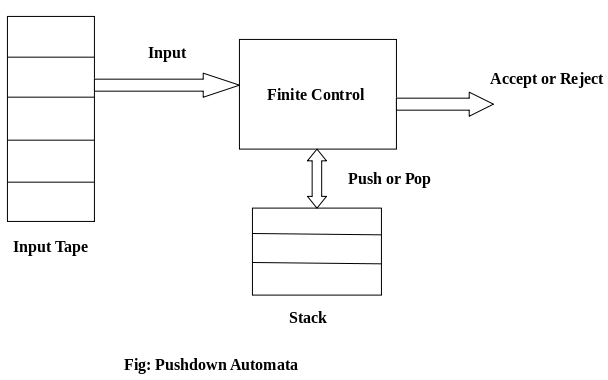
PDA Components:Input tape: The input tape is divided in many cells or symbols. The input head is read-only and may only move from left to right, one symbol at a time. Finite control: The finite control has some pointer which points the current symbol which is to be read. Stack: The stack is a structure in which we can push and remove the items from one end only. It has an infinite size. In PDA, the stack is used to store the items temporarily. Formal definition of PDA:The PDA can be defined as a collection of 7 components: Q: the finite set of states ∑: the input set Γ: a stack symbol which can be pushed and popped from the stack q0: the initial state Z: a start symbol which is in Γ. F: a set of final states δ: mapping function which is used for moving from current state to next state. Instantaneous Description (ID)ID is an informal notation of how a PDA computes an input string and make a decision that string is accepted or rejected. An instantaneous description is a triple (q, w, α) where: q describes the current state. w describes the remaining input. α describes the stack contents, top at the left. Turnstile Notation:⊢ sign describes the turnstile notation and represents one move. ⊢* sign describes a sequence of moves. For example, (p, b, T) ⊢ (q, w, α) In the above example, while taking a transition from state p to q, the input symbol 'b' is consumed, and the top of the stack 'T' is represented by a new string α. Example 1:Design a PDA for accepting a language {anb2n | n>=1}. Solution: In this language, n number of a's should be followed by 2n number of b's. Hence, we will apply a very simple logic, and that is if we read single 'a', we will push two a's onto the stack. As soon as we read 'b' then for every single 'b' only one 'a' should get popped from the stack. The ID can be constructed as follows: Now when we read b, we will change the state from q0 to q1 and start popping corresponding 'a'. Hence, Thus this process of popping 'b' will be repeated unless all the symbols are read. Note that popping action occurs in state q1 only. After reading all b's, all the corresponding a's should get popped. Hence when we read ε as input symbol then there should be nothing in the stack. Hence the move will be: Where PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2}) We can summarize the ID as: Now we will simulate this PDA for the input string "aaabbbbbb". Example 2:Design a PDA for accepting a language {0n1m0n | m, n>=1}. Solution: In this PDA, n number of 0's are followed by any number of 1's followed n number of 0's. Hence the logic for design of such PDA will be as follows: Push all 0's onto the stack on encountering first 0's. Then if we read 1, just do nothing. Then read 0, and on each read of 0, pop one 0 from the stack. For instance: 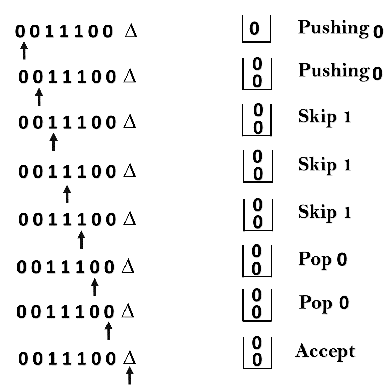
This scenario can be written in the ID form as: Now we will simulate this PDA for the input string "0011100".
Next TopicPDA Acceptance
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










