Bernoulli number in JavaBernoulli numbers are the special type of numbers that plays an important role in number theory and analysis. These numbers are mainly used in series expansions of several trigonometric, gamma, hyperbolic functions, etc. Nth Bernoulli number is denoted by Bn that can be defined by the following exponential generating function: 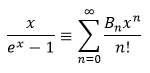
Bernoulli numbers arise in the expansion of the series of trigonometric functions. We have two different definitions for the Bernoulli numbers. The Bernoulli numbers are written as , as defined in the modern usage or the National Institute of Standards and Technology convention. It is also referred to as "even-index" Bernoulli numbers. The Bernoulli numbers are written as , as per the definition defined in the old literature. In both of the cases, each Bernoulli number is a special case of the Bernoulli polynomials: Bn (x) OR Bn* (x) with Bn=Bn (0) AND Bn* (0) We also denote the Bell number and Bell polynomial as Bn and Bn (x), respectively. So, we should not be confused with both of them. We can define the Bernoulli number Bn by using the following contour integral: 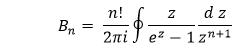
AlgorithmThe algorithm to find the "second Bernoulli numbers" is as follows: Let's implement the code to get N Bernoulli numbers in Java. Before writing the logic to get Bernoulli numbers, we create BigRational.java class that performs the necessary operations for BigDecimal and BigInteger and return the result. BigRational.java BernoulliNumber.java Output: 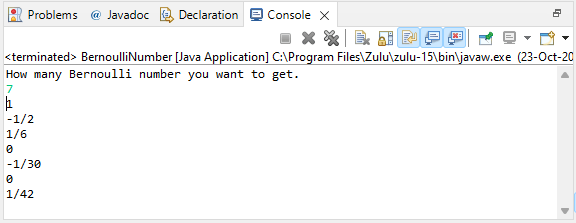
Next TopicCake Number in Java
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










