Cake Number in Java

In this section, we will learn about finding the cake number in Java. The cake number CK_nrepresents the maximum number of pieces a cake can be divided with the help of n planar cuts. The tridimensional version of the pancake numbers is the cake numbers.

In general,

CK_n= (n³ + 5 *n + 6) / 6 where n >= 0

Thus,

For n = 0,

CK₀= (0³+ 5 * 0 + 6) / 6 = (6) / 6 = 6 / 6 = 1

For n = 1,

CK₁= (1³+ 5 * 1 + 6) / 6 = (1 + 5 + 6) / 6 = 12 / 6 = 2

For n = 2,

CK₂= (2³+ 5 * 2 + 6) / 6 = (8 + 10 + 6) / 6 = 24 / 6 = 4

For n = 3,

CK₃= (3³+ 5 * 3 + 6) / 6 = (27 + 15 + 6) / 6 = 48 / 6 = 8

For n = 4,

CK₄= (4³+ 5 * 4 + 6) / 6 = (64 + 20 + 6) / 6 = 90 / 6 = 15

For a = 5,

CK₅= (5³+ 5 * 5 + 6) / 6 = (125 + 25 + 6) / 6 = 156 / 6 = 26

Implementation

Let's see how one can implement the above mathematical formula. Observe the following example.

FileName: CakeNumberExample1.java

public class CakeNumberExample1
{
// a method that finds the value of b ^ e
int pow(int b, int e)
{
// anything whose power is 0 is 1
if(e == 0)
{
return 1;
}

// it will store the result
int ans = 1;
while(true)
{

if(e % 2 == 1)
{
e = e - 1;
ans = ans * b;
if(e == 0)
{
return ans;
}
}
b = b * b;
e = e / 2;
}
}
public int findCakeNo(int n)
{
// finding n ^ 3
int x = pow(n, 3);
// finding 5 * n
int y = 5 * n;
// finding the cake number
// computing (n ^ 3 + 5 * n + 6) / 6
int no = (x + y + 6) / 6;
return no;
}
// main method
public static void main(String argvs[])
{
// creating an object of the class CakeNumberExample1
CakeNumberExample1 obj = new CakeNumberExample1();
System.out.println("The first 30 cake numbers are: ");
for(int i = 0; i < 30; i++)
{
// invoking the method findCakeNo()
int num = obj. findCakeNo(i);
System.out.print(num + " ");
}
}
}

Output:

The first 30 cake numbers are: 
1 2 4 8 15 26 42 64 93 130 176 232 299 378 470 576 697 834 988 1160 1351 1562 1794 2048 2325 2626 2952 3304 3683 4090

Using Recursion

The cake numbers can also be found using recursion. However, to find cake numbers using recursion, we must know the recursive formula of it.

CK₀= 1, for n = 0

CK₁= 2, for n = 1

CK_n = ^{n + 1}C₃ + n + 1, for n >= 2

Thus,

For n = 2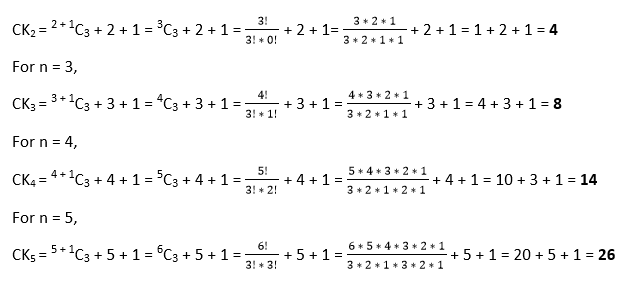

Implementation

Let's see how one can implement the above mathematical formula. Observe the following example.

FileName: CakeNumberExample2.java

public class CakeNumberExample2
{
public int findCakeNo(int n, int r)
{
// handling the base case nC0 = 1
if(r == 0)
{
    return 1;
}
// handling the base case nC1 = n
else if(r == 1)
{
    return n;
}
// handling the base case nCn = 1
else if( n == r )
{
    return 1;
}
// nCr = ( n / r ) * (n - 1)C(r - 1)
int ans = findCakeNo(n - 1, r - 1);
ans = (ans * n) / r;
return ans;

}
// main method
public static void main(String argvs[])
{
// creating an object of the class CakeNumberExample2
CakeNumberExample2 obj = new CakeNumberExample2();
System.out.println("The first 30 cake numbers are: ");

for(int i = 0; i < 30; i++)
{
int num = 1;
// first cake number
if(i == 0)
{
num = 1;    
}
// second cake number
else if(i == 1)
{
num = 2;
}
// invoking the method findCakeNo()
num = obj. findCakeNo(i + 1, 3) + i + 1;
System.out.print(num + " ");
}
}
}

Output:

The first 30 cake numbers are: 
1 2 4 8 15 26 42 64 93 130 176 232 299 378 470 576 697 834 988 1160 1351 1562 1794 2048 2325 2626 2952 3304 3683 4090

Using Iteration

The cake numbers can also be found using iteration. We will use loops to find the cake numbers with the help of a two-dimensional array. Observe the following program.

FileName: CakeNumberExample3.java

public class CakeNumberExample3
{

// main method
public static void main(String argvs[])
{
// array for storing combinations of 
// numbers
int arr[][] = new int[31][4];

// nCr, for r = 0 is always 1
for(int i = 0; i < 31; i++)
{
arr[i][0] = 1;
}


// for finding nCr where r != 0
for(int i = 1; i < 31; i++)
{
for(int j = 1; j <= 3 && j <= i; j++)
{
if(i == j)
{
arr[i][j] = 1;
}
else
{
// nCr = (n - 1)C(r - 1) + (n - 1)Cr
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
}
}

System.out.println("The first 30 cake numbers are: ");

for(int i = 0; i < 30; i++)
{
int num = 1;

// first cake number
if(i == 0)
{
num = 1;    
}

// second cake number
else if(i == 1)
{
num = 2;
}

// finding the remaining cake numbers using the
// combinations result stored in the array arr[][]

// computing (n + 1)C3 + n + 1 
num = arr[i + 1][3] + i + 1;
    
System.out.print(num + " ");
}
}
}

Output:

The first 30 cake numbers are: 
1 2 4 8 15 26 42 64 93 130 176 232 299 378 470 576 697 834 988 1160 1351 1562 1794 2048 2325 2626 2952 3304 3683 4090

Another Approach

Apart from the above-discussed approach, there is another approach to compute the cake numbers using combinations. Observe the following mathematical statement.

CK₀= 1, for

CK₁= 2, for

CK₂= 4, for

CK_n = ⁿC₃ + ⁿC₂ + ⁿC₁ + ⁿC₀, for n >= 3

Thus,

For n = 3,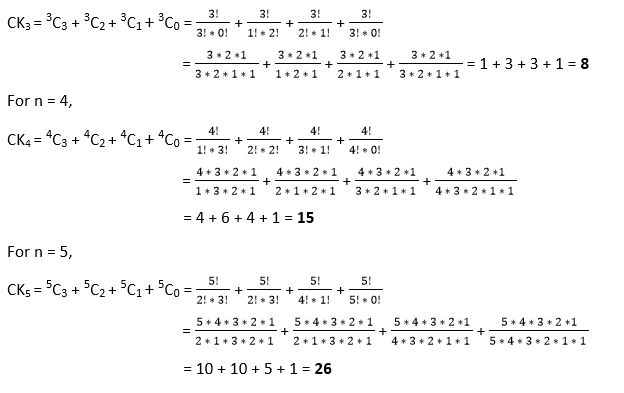

Implementation

Let's see the recursive as well as the iterative implementation of the above formula to find the cake numbers in the code mentioned below.

FileName: CakeNumberExample4.java

public class CakeNumberExample4
{

int arr[][] = new int[31][4];

public void fill()
{
    
// nCr, for r = 0 is always 1
for(int i = 0; i < 31; i++)
{
arr[i][0] = 1;
}


// for finding nCr where r != 0
for(int i = 1; i < 31; i++)
{
for(int j = 1; j <= 3 && j <= i; j++)
{
if(i == j)
{
arr[i][j] = 1;
}
else
{
// nCr = (n - 1)C(r - 1) + (n - 1)Cr
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
}
}

}

// finding xCy
public int findCakeNumRecursive(int x, int y)
{

// xCy = 1, for y = x
if(x == y)
{
return 1;
}

// xCy = 1, for y = 0
else if(y == 0)
{
return 1;
}

else
{
int ans = findCakeNumRecursive(x - 1, y - 1);
ans = (ans * x) / y;
return ans;
}

}


// finding xCy iteratively
public int findCakeNumIterative(int x, int y)
{

// xCy = 1, for y = x
if(x == y)
{
return 1;
}

// xCy = 1, for y = 0
else if(y == 0)
{
return 1;
}

else
{
int ans = arr[x][y];
return ans;
}

}


// main method
public static void main(String argvs[])
{
    
// creating an object of the class CakeNumberExample4
CakeNumberExample4 obj = new CakeNumberExample4();

System.out.println("The first 30 cake numbers are: ");

for(int i = 0; i < 30; i++)
{
int num = 1;

// first cake number
if(i == 0)
{
num = 1;    
}

// second cake number
else if(i == 1)
{
num = 2;
}
else if(i == 2)
{
    num = 4;
}
else
{
// recursively finding iC3, iC2, iC1, iC0
num = obj.findCakeNumRecursive(i, 3) +
            obj.findCakeNumRecursive(i, 2) +
            obj.findCakeNumRecursive(i, 1) +
            obj.findCakeNumRecursive(i, 0);
       
}

System.out.print(num + " ");

}

System.out.println("\n ");

obj.fill();


System.out.println("The first 30 cake numbers are: ");

for(int i = 0; i < 30; i++)
{
int num = 1;

// first cake number
if(i == 0)
{
num = 1;    
}

// second cake number
else if(i == 1)
{
num = 2;
}

else
{
// iteratively finding iC3, iC2, iC1, iC0
num = obj.findCakeNumIterative(i, 3) +
            obj.findCakeNumIterative(i, 2) +
            obj.findCakeNumIterative(i, 1) +
            obj.findCakeNumIterative(i, 0);  
}

System.out.print(num + " ");

}
}
}

Output:

The first 30 cake numbers are: 
1 2 4 8 15 26 42 64 93 130 176 232 299 378 470 576 697 834 988 1160 1351 1562 1794 2048 2325 2626 2952 3304 3683 4090 

The first 30 cake numbers are: 
1 2 4 8 15 26 42 64 93 130 176 232 299 378 470 576 697 834 988 1160 1351 1562 1794 2048 2325 2626 2952 3304 3683 4090

Next TopicCompare time in Java

← prev next →