Boyer Moore Java

Boyer-Moore algorithm is a string searching or matching algorithm developed by Robert S. Boyer and J Strother Moore in 1977. It is a widely used and the most efficient string-matching algorithm. It is much faster than the brute-force algorithm. In this section, we will discuss the Boyer-Moore algorithm, features, and its implementation in a Java program. It runs in time O(nm+s) complexity. The worst-case is:

T=ssssssss……………ssssssss

P=psssssssss

The above sequence may occur in images and DNA sequences.

Features of Boyer Moore Algorithm

It compares character by character from right to left;
The preprocessing phase in O(m+)time and space complexity.
The complexity of the searching phase is O(mn).
In the worst case (when searching for a non-periodic pattern), it makes 3n text character comparisons.
Its best performance complexity is O(n / m).

The algorithm is based on the following two heuristics:

Looking-Glass Heuristics
Character-Jump Heuristics

Let's understand the working of the Byer-Moore algorithm.

Working of Boyer-Moore Algorithm

The algorithm starts tracing characters from the rightmost character of the given pattern and moves towards the left. In case of any mismatch and complete matching of the pattern, it uses two pre-computed functions that shift the characters to the right and left, respectively. These two precomputed shift functions are called the good-suffix shift (or matching shift) and the bad-character shift (or occurrence shift).

Note: For matching the pattern, align characters in left to right order and compare characters in right to left order.

Bad Character Shift

When a mismatch occurs, skip alignment until one of the following conditions does not meet:

Mismatch becomes a match
P moves past mismatch character

For example, consider the following text (T) and pattern (P) given below.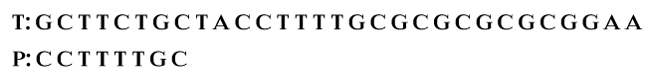

Let's start matching the pattern.

Step 1: Align characters in left to right fashion and compare characters in right to left order.

We see that the last three characters of P matched with the characters in T. The fourth character (T) does not match. According to the rule discussed above, skip alignment until a mismatch becomes a match. Since the seventh character (C) in P matched with C in T.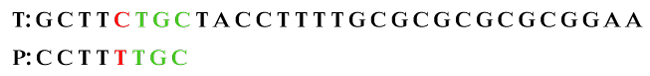

Step 2: Skip three characters to the right to matching the pattern.

After shifting, again compare the characters from right to left. The first character is matched. We observe that the character A does not occur in the left of P. In this case, P moves to the past mismatch character (A) in T.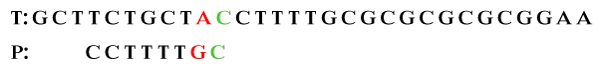

Step 3: Move P past mismatch character, we get: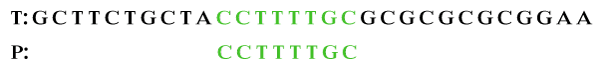

The pattern is matched.

Note: The bad-character shift can be negative. Since for shifting the characters, the Boyer-Moore algorithm applies the maximum (skip characters) between the good-suffix shift and bad-character shift.

Good-Suffix Shift

Let, t substring matched by inner loop, then skip characters until:

There are no mismatches between P and t.
P moves past t.

For example, consider the following pattern.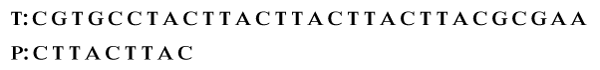

Step 1: Compare characters from right to left. We see that the last three characters of P matched with characters in T denoted with t.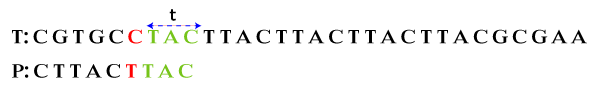

Step 2: Skip characters until there is no match between P and t. We observe that the first four characters (from left to right) of P (C T T A C) match with the last five characters in t.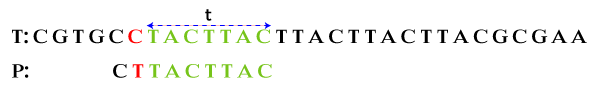

Step 3: Skip three alignments to get the match. Therefore, we get the match.

The above two-shift functions can be defined as follows:

The good-suffix shift function is stored in a table called bmGs of size m+1. The computation of the table bmGs use a table suff defined as follows:

The bad-character shift function is stored in a table bmBc of size σ. For c in ∑:

Boyer Moore Pattern Matching Example

Consider the following pattern.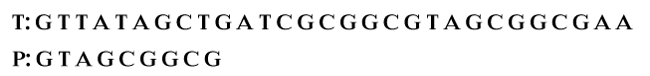

Let's start matching.

Step 1: Compare characters from right to left. We see that the first character is mismatched i.e. G does not match with T.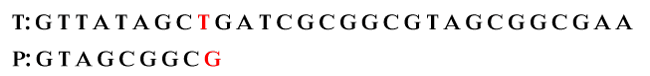

Step 2: Now, skip the characters until we found a match. A match is found after six characters. Here, the good suffix shift rule will not apply.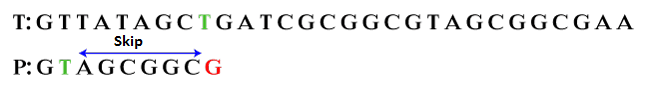

bc: 6, gs: 0

According to bad character shift, P moves past mismatch character (i.e. G).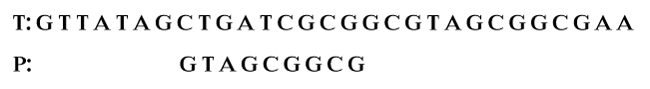

Step 3: Again, compare characters from right to left. We see that the first three characters of P matched (t) with T and the fourth one is not matched.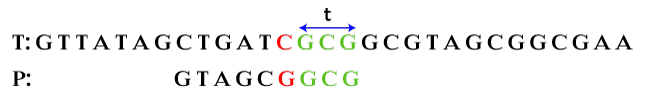

Here, we can apply both functions i.e. bad character suffix and good character suffix. If we apply the bad character suffix, it skips only one character. If we apply the good character suffix, it skips two alignments. Therefore, we will apply the good character suffix because the algorithm states, skip more alignments. Hence, we skip two alignments.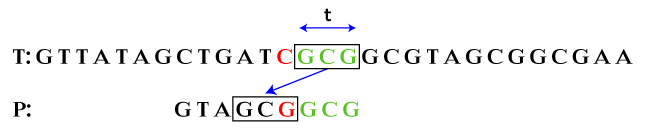

bc: 0, gs: 2

After shifting alignment by three characters, we get: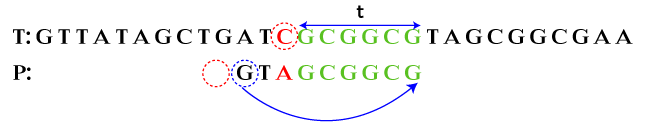

bc: 2, gs: 7

Here, we observe that C does not appears in the left of P. Therefore, bad character alignment skips two alignments and the good character alignments skips the seven alignments.

Step 4: After shifting characters, we see that the string is matched.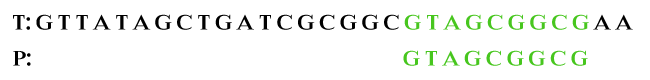

In the above pattern, we have skipped 15 alignments and 11 characters of T were ignored.

Boyer Moore Preprocessing Phases

Pre-calculated skips for the pattern T: A A T C A A T A G C and P: T C G C can be defined as follows. In the above pattern, we have used the bad character shift function.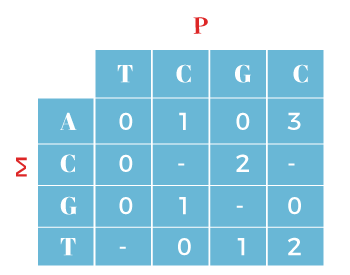

Above table defines the number of skip alignments (characters).

Boyer Moore Algorithm Pseudo Code

BoyerMooreMatch(T, P, ?)
L<- lastOccurenceFunction(P, ?)
i <- m-1
j <- m-1
repeat
                    if T[i]=P[j]
                             if j=0
                                  return i {match at i}
                             else
                                  i <- i-1
                                  j <- j-1
                    else
                         {character-jump}
                         L<-L[T[i]]
                         i <- i +m -min(j, 1+ l)
                         j <- m-1
until i>n-1
return-1 {no match}

Pattern Searching Java Program

Let's see the pattern searching Java program. In the following program, we have implemented the brute-force string searching algorithm.

PatternSearchingExample.java

import java.util.HashMap;
import java.util.Map;
public class PatternSearchingExample
{
/** 
* @param text -- trace the text to see if it contains pattern
* @param pattern -- look for this text inside the text parameter
* @return -- return index of the first match or -1 if not found
*/
public static int findBruteForce(char[] text, char[] pattern) 
{
System.out.println("Brute force looking for " + String.valueOf(pattern) + " in " + String.valueOf(text));
int n = text.length;
int m = pattern.length;
//checks if the string is empty
if (m == 0) return 0;
//brute force it -- loop over all characters in text O(n)
for (int i=0;i<=n-m;i++) 
{ //index into the text
//loop over all characters in pattern while characters match O(m)
//index into the pattern
int k = 0; 
while (k<m && text[i+k] == pattern[k]) 
{
k++;
}
//if at end of the pattern, then found match starting at index i in text
if (k==m) 
{
System.out.println("\tFound match in the given text at index " + i);
return i;
}
}
//if match not found
System.out.println("\tNo match found in the given text.");
return -1;
}
/**

* @param text -- search this text to see if it contains pattern
* @param pattern -- look for this text inside the text parameter
* @return -- return index of the first match or -1 if not found
*/
public static int findBoyerMoore(char[] text, char[] pattern) 
{
System.out.println("Boyer-Moore looking for " + String.valueOf(pattern) + " in " + String.valueOf(text));
int n = text.length;
int m = pattern.length;
// Test for empty string
if (m == 0) return 0;
// Initialization, create Map of last position of each character = O(n)
Map<Character, Integer> last = new HashMap<>();
for (int i = 0; i < n; i++) 
{
// set all chars, by default, to -1    
last.put(text[i], -1);   
}        
for (int i = 0; i < m; i++) 
{
// update last seen positions    
last.put(pattern[i], i); 
}
//Start with the end of the pattern aligned at index m-1 in the text. 
//index into the text
int i = m - 1;  
// index into the pattern
int k = m - 1;  
while (i < n) 
{ 
if (text[i] == pattern[k]) 
{
// match! return i if complete match; otherwise, keep checking    
if (k == 0) 
{
System.out.println("\tFound match in the given text at index " + i);
return i; 
}
i--; k--;
} 
else 
{ // jump step + restart at end of pattern
//iterate over text 
i += m - Math.min(k, 1 + last.get(text[i]));  
//move to end of pattern
k = m - 1; 
}
}
System.out.println("\tNo match found in the given text.");
// not found
return -1; 
}
public static void main(String args[]) 
{
char[] text = "abcfefabddef".toCharArray();
char[] pattern = "abddef".toCharArray();
//function calling
findBruteForce(text,pattern);
findBoyerMoore(text,pattern);        
}
} 

Output:

Brute force looking for abddef in abcfefabddef
	Found match in the given text at index 6
Boyer-Moore looking for abddef in abcfefabddef
	Found match in the given text at index 6

Let's implement the algorithm in a Java program.

Boyer Moore Java Program

Let's implement the Boyer-Moore algorithm and search pattern through a Java program.

BoyerMooreImplementation.java

public class BoyerMooreImplementation
{
static int NO_OF_CHARS = 256; 
static int max (int a, int b) 
{ 
return (a > b)? a: b; 
} 
static void badCharHeuristic( char []str, int size, int badchar[]) 
{ 
int i; 
for (i = 0; i < NO_OF_CHARS; i++) 
badchar[i] = -1; 
for (i = 0; i < size; i++) 
badchar[(int) str[i]] = i; 
} 
static void search( char txt[],  char pat[]) 
{ 
int m = pat.length; 
int n = txt.length; 
int badchar[] = new int[NO_OF_CHARS]; 
//function calling
badCharHeuristic(pat, m, badchar); 
int s = 0;  
while(s <= (n - m)) 
{ 
int j = m-1; 
while(j >= 0 && pat[j] == txt[s+j]) 
j--; 
if (j < 0) 
{ 
System.out.println("Patterns occur at character = " + s); 
s += (s+m < n)? m-badchar[txt[s+m]] : 1; 
} 
else
s += max(1, j - badchar[txt[s+j]]); 
} 
} 
public static void main(String args[]) 
{ 
//text in which pattern occurs
char txt[] = "123651266512".toCharArray(); 
//pattern to search
char pat[] = "12".toCharArray(); 
search(txt, pat); 
} 
}

Output:

Patterns occur at character = 0
Patterns occur at character = 5
Patterns occur at character = 10

Let's see another Java program in which we have implemented different logic for pattern searching. The following program checks if the specified pattern found in the text.

BoyerMooreExample.java

public class BoyerMooreExample
{
public static void main(String args[]) 
{
        System.out.println("Matching Pattern");
        test("aabbccdef", "cde", 0);
        test("zzzzaaapppxyzabc", "pqrs", 1);
        test("mango", "ngo", 2);
        test("abc", "d", -1);
        test("catdog", "tdo", 2);
        test("pqrsabcdxyzamnop", "cdxyza", 1);
        test("cool", "", 0);
        test("", "car", -1);
}
    public static void test(String text, String word, int exp) 
    {
        char[] textC = text.toCharArray();
        char[] wordC = word.toCharArray();
        int result = bm(textC, wordC);
        if(result == exp)
            System.out.println("Pattern Matched");
        else 
        {
            System.out.println("Pattern Not Matched");
            System.out.println("\ttext: " + text);
            System.out.println("\tword: " + word);
            System.out.println("\texp: " + exp + ", res: " + result);
        }//end of else
    }//end of function
    public static int[] makeD1(char[] pat) 
    {
        int[] table = new int[255];
        for(int i=0; i<255; i++)
            table[i] = pat.length;
        for(int i=0; i<pat.length-1; i++)
            table[pat[i]] = pat.length-1-i;
        return table;
    }//end of function
    public static boolean isPrefix(char[] word, int pos) 
    {
        int suffixlen = word.length - pos;
        for(int i=0; i<suffixlen; i++)
            if(word[i] != word[pos+i])
                return false;
        return true;
    }//end of function
    public static int suffix_length(char[] word, int pos) 
    {
        int i;
        for(i=0; ((word[pos-i] == word[word.length-1-i]) & (i < pos)); i++)
            {
                
            }//end of for loop
        return i;
    }//end of function 
    public static int[] makeD2(char[] pat) 
    {
        int[] delta2 = new int[pat.length];
        int p;
        int last_prefix_index = pat.length - 1;
        for(p = pat.length-1; p>=0; p--) 
        {
            if(isPrefix(pat, p+1))
                last_prefix_index = p+1;
            delta2[p] = last_prefix_index + (pat.length-1-p);
        }//end of for loop
        for(p=0; p<pat.length-1; p++) 
        {
            int slen = suffix_length(pat, p);
            if(pat[p-slen] != pat[pat.length-1-slen])
                delta2[pat.length-1-slen] = pat.length-1-p+slen;
        }//end of for loop
        return delta2;
    }//end of function
    public static int bm(char[] string, char[] pat) 
    {
        int[] d1 = makeD1(pat);
        int[] d2 = makeD2(pat);
        int i = pat.length-1;
        while(i < string.length) 
        {
            int j = pat.length-1;
            while(j>=0 && (string[i] == pat[j])) 
            {
                i--; //decrement i by 1
                j--; //decrement j by 1
            }//end of while
            if(j < 0)
                return (i+1);
            i += Math.max(d1[string[i]], d2[j]);
        } //end of while
        return -1;
    }//end of function
}

Output:

Pattern Not Matched
	text: aabbccdef
	word: cde
	exp: 0, res: 5
Pattern Not Matched
	text: zzzzaaapppxyzabc
	word: pqrs
	exp: 1, res: -1
Pattern Matched
Pattern Matched
Pattern Matched
Pattern Not Matched
	text: pqrsabcdxyzamnop
	word: cdxyza
	exp: 1, res: 6
Pattern Matched
Pattern Matched

Next TopicJava Security Framework

← prev next →