Catalan Number in JavaIn this section, we will learn what is a Catalan number and also create Java programs to check if the given number is a Catalan number or not. The Catalan number program is frequently asked in Java coding interviews and academics. There are many interesting problems that can be solved using the Catalan number. Mathematically, the Catalan numbers are defined as, 
Steps to Find the Catalan NumbersStep 1: Assign a non-negative integer to the variable n. Step 2: Find the value of 2nCn, where n is determined in step 1. Step 3: Divide the value found in step 2 by n+1. The resultant that we get after the division is a Catalan number. Example Catalan Number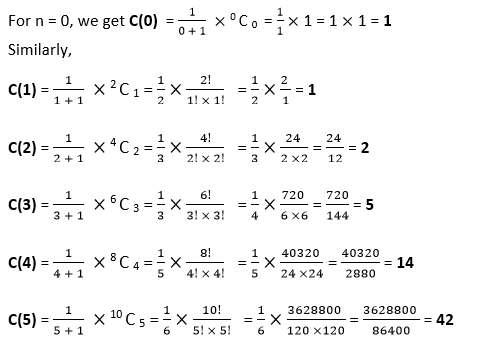
The following diagram shows Catalan numbers for numbers from 0 to 3. 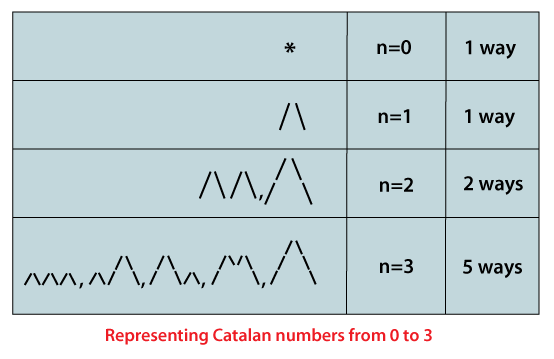
Catalan Number Java ProgramThe following program is based on the steps defined above. FileName: CatalanNumberExample.java Output: For n = 0, Catalan number is 1 For n = 1, Catalan number is 1 For n = 2, Catalan number is 2 For n = 3, Catalan number is 5 For n = 4, Catalan number is 14 For n = 5, Catalan number is 42 For n = 6, Catalan number is 132 For n = 7, Catalan number is 429 For n = 8, Catalan number is 1430 For n = 9, Catalan number is 4862 For n = 10, Catalan number is 16796 Catalan Numbers Using Recursive ApproachWe can also find the Catalan number by using the recursive approach. It can be defined as follows. 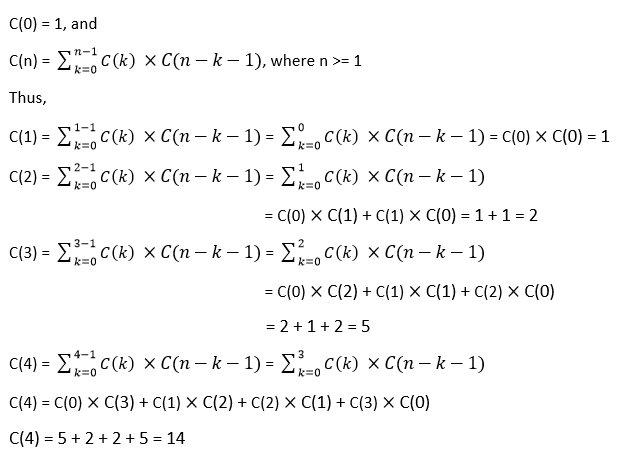
Similarly, we can find other values too. Note that while finding the Catalan number for the next term, use the values of the previous terms. For example, the value of C(4) is dependent on C(0), C(1), C(2), and C(3). Let's implement the recursive approach in a Java program. FileName: CatalanNumberExample1.java Output: For number = 0, the Catalan number is 1 For number = 1, the Catalan number is 1 For number = 2, the Catalan number is 2 For number = 3, the Catalan number is 5 For number = 4, the Catalan number is 14 For number = 5, the Catalan number is 42 For number = 6, the Catalan number is 132 For number = 7, the Catalan number is 429 For number = 8, the Catalan number is 1430 For number = 9, the Catalan number is 4862 For number = 10, the Catalan number is 16796 Using Dynamic ProgrammingThe recursive program written above takes a lot of time to find the Catalan numbers. It is because we are using recursion inside the Java for-loop. Therefore, we need to find another approach that takes less time as compared to the above one. By using dynamic programming, we can reduce time. In this approach, we will be shifting from recursive to iterative approach, as the iterative approach is much faster. Observe the following program for the same. FileName: CatalanNumberExample2.java Output: For number = 0, the Catalan number is 1 For number = 1, the Catalan number is 1 For number = 2, the Catalan number is 2 For number = 3, the Catalan number is 5 For number = 4, the Catalan number is 14 For number = 5, the Catalan number is 42 For number = 6, the Catalan number is 132 For number = 7, the Catalan number is 429 For number = 8, the Catalan number is 1430 For number = 9, the Catalan number is 4862 For number = 10, the Catalan number is 16796 Explanation: The problem with the recursive approach was that it was calculating the same subproblem again and again. It leads to more time consumption. Therefore, we have used an array, arr, to store the solution of the subproblem. Hence, whenever there is a need of the solution of a subproblem, we can used it from the array arr. Thus, we have saved the computational time of repeated subproblems. Application of Catalan NumbersAs discussed above, one can solve many interesting problems using Catalan numbers a few of them are mentioned below. 1) For n > 0, the number of unique Binary Search Trees is equal to the Catalan number C(n), where n is the number of nodes present in the Binary Search Trees. 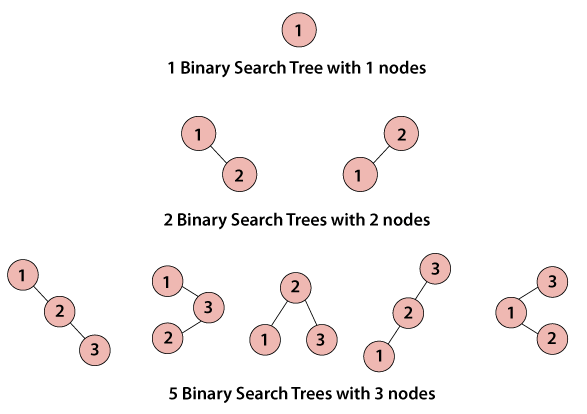
2) For n > 0, the total number of n pair of parentheses that are correctly matched is equal to the Catalan number C(n). 
3) The total number of chords drawn on a circle using 2 × n points such that no two chords intersect or touch each other is given by the Catalan number C(n). 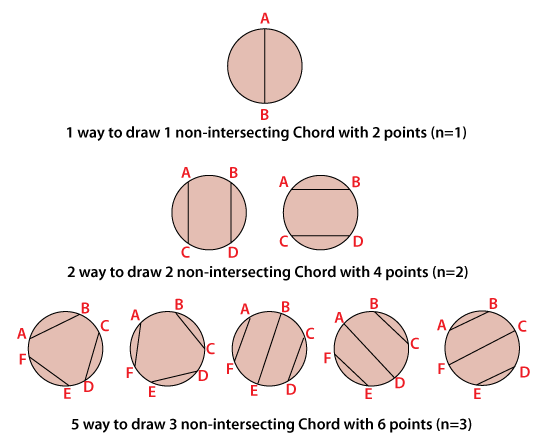
Next TopicPartition Number in Java
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










