Partition Number in Java

In this section, we will learn what is a partition number and also create Java programs to check if the given number is a partition number or not. The partition number program is frequently asked in Java coding interviews and academics.

Partition Number

In combinatorics and number theory, partitioning a number K (greater than 0) means writing the number K using the sum of positive integers. Partition Number is also known as integer partition. Note that the ordering of the summands does not matter in doing the partition. Let's understand it with the help of an example.

Approach

We display all the partitions in sorted order and the numbers within a partition are also printed in the sorted order. The concept is to achieve the next partition with the help of the values in the current partition.

We store each partition in the array ptt[]. We initialize the array ptt[] as K, where K is an input number. In each iteration, first, we print ptt[], and then update the array ptt[] to keep the next partition. Hence, our problem is reduced to find the next partition from the current partition.

Steps to Find Next Partition Number with the help of Current Position

The current partition is present in the array ptt[], and its size is also known. We are required to update ptt[] to keep the next partition. Values in the ptt[] should be sorted in the non-increasing order.

Step 1: Look for the rightmost non-one value in the array ptt[] and keep the count of 1's encountered before the non-one value in a variable r_val (It shows the sum of the values on the right side that needs to be updated). Suppose, the index of the non-one value be i.

Step 2: Reduce the value of ptt[i] by one and increase r_val by 1. Now there can be the following two cases:

If ptt[i] is equal to or more than r_val. It is a simple case (we have got the sorted order in the new partition). Put r_val at ptt[i + 1] and ptt[0…i + 1] is the new partition.
Otherwise (It is an interesting case, take the initial ptt[] as {3, 1, 1, 1}, ptt[i] is decreased from 3 to 2, r_val is increased from 3 to 4, hence, the next partition will be {2, 2, 2}).

Step 3: Copy ptt[i] to the next position, increment i and reduce the count by ptt[i] while ptt[i] is less than r_val. Eventually, put r_val at ptt[i + 1] and p[0…i + 1] is the new partition. The step is like splitting r_val in the terms of ptt[i] (4 is splitted in 2's).

Examples of Partition Numbers

Let K = 4, then K can be written as,

4 = 4 First way

3 + 1 = 4 Second way (1 + 3 is not considered, as ordering of summands has no impact in the partition)

2 + 2 = 4 Third way

2 + 1 + 1 = 4 Fourth way (Similarly, 1 + 2 + 1, 1 + 1 + 2 are not considered)

1 + 1 + 1 + 1 = 4 Fifth way

Thus, there are five unique ways to split the number 4. The following figure shows the partitioning of numbers from 1 to 6.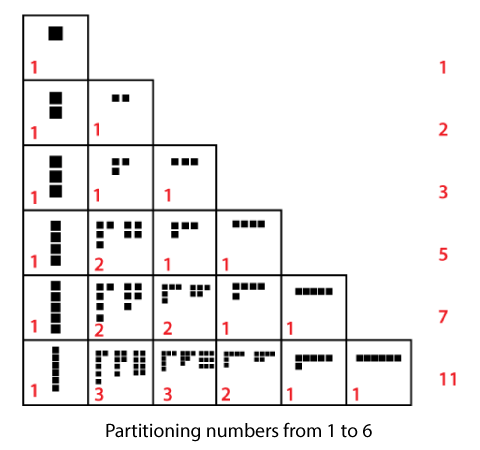

Partition Number Java Program

Let's observe the Java program.

FileName: PartitionNumberExample.java

// A Java program that generates all the unique
// partitions of an integer, which is greater than 0

public class PartitionExample
{
// A method to display an array ptt[] of size s
public void displayArray(int ptt[], int s)
{
for (int j = 0; j < s; j++)
{
System.out.print(ptt[j] + " ");
}
System.out.println();
}
	
// a method to generate all the unique partitions of the number no
public void printAllUniqueParts(int no)
{
int ptt[] = new int[no]; // An array to store a partition
int indLast = 0; // Index of the last element in a partition
ptt[indLast] = no; // Initialize first partition as number itself

// The while loop first displays the current partition and then produces the next
// partition. The loop terminates when there are all 1s in the current partition
while(true)
{
// display the current partition
displayArray(ptt, indLast + 1);

// Produce the next partition

// Look for the rightmost non-one value in the array ptt[]. Also, update the
// r_val so that one knows that how much value are there to be accommodated
int r_val = 0;
while (indLast >= 0 && ptt[indLast] == 1)
{
r_val = r_val + ptt[indLast];
indLast = indLast - 1;
}

// if indLast < 0, then it means all the values in the currrent 
// partition are 1. Hence, further partition is not possible. 
// Therefore, terminate the loop.
if (indLast < 0) break;

// Reduce the ptt[indLast] by 1 in order to adjust the r_val
ptt[indLast] = ptt[indLast] - 1;
r_val = r_val + 1;


// If r_val is more, then the non-increasing order of sorting is getting violated. 
// Therefore, split the r_val in different values of size ptt[indLast] and copy those values // at the different positions after ptt[indLast]
while (r_val > ptt[indLast])
{
ptt[indLast + 1] = ptt[indLast];
r_val = r_val - ptt[indLast];
indLast = indLast + 1;
}

// Copy the r_val to the next position and increment the position
ptt[indLast + 1] = r_val;
indLast = indLast + 1;
}
}

// main method
public static void main (String[] argvs)
{
// creating an object of the class PartitionExample
PartitionExample obj = new PartitionExample();

System.out.println("All the Unique Partitions of 2 are: ");
obj.printAllUniqueParts(2);
System.out.println();

System.out.println("All the Unique Partitions of 3 are: ");
obj.printAllUniqueParts(3);
System.out.println();

System.out.println("All the Unique Partitions of 4 are: ");
obj.printAllUniqueParts(4);
System.out.println();

System.out.println("All the Unique Partitions of 5 are: ");
obj.printAllUniqueParts(5);
System.out.println();
}
}

Output:

All the Unique Partitions of 2 are: 
2 
1 1 

All the Unique Partitions of 3 are: 
3 
2 1 
1 1 1 

All the Unique Partitions of 4 are: 
4 
3 1 
2 2 
2 1 1 
1 1 1 1 

All the Unique Partitions of 5 are: 
5 
4 1 
3 2 
3 1 1 
2 2 1 
2 1 1 1 
1 1 1 1 1

Explanation: The Java program is based on the approach discussed above. The key here is to maintain the sorting in non-increasing order while doing the partition, and when there is violation follow the step 2 and step 3 defined above before the beginning of the program.

Next TopicPowerful Number in Java

← prev next →