Chromatic Number in Java

The chromatic numbers are generally used in the coloring of graph nodes with some constraints. Chromatic Numbers in Java tell the minimum number of unique colors required to color all the nodes of a graph such that any two adjacent nodes do not have the same color. It can be used in many applications. In this section, we will implement the greedy approach to find the chromatic number for a graph.

Steps to Find the Chromatic Numbers

Step 1: Assign the first color to the first node of the graph.

Step 2: Do the following for the remaining N - 1 node.

Consider the currently picked node and assign a color to it with the lowest numbered color. Provided that the color has not been applied on any of the previously colored nodes adjacent to it. If all colors that are previously used appear on the nodes that are adjacent to, assign a new color to it.

Examples of Chromatic Number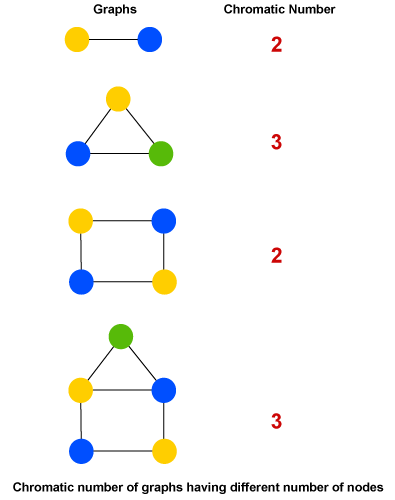

Chromatic Number Java Program

The following program is based on the steps defined above.

FileName: Graphs.java

// A Java program that implements the greedy algorithm for the graph coloring
import java.util.LinkedList;
import java.util.*;
import java.io.*;

// The class shows an undirected graph using an adjacency list
public class Graphs
{
private int N; // No. of nodes
private LinkedList<Integer> adjList[]; //Adjacency List

//Constructor
Graphs(int n)
{
N = n;
adjList = new LinkedList[n];
for (int i = 0; i < n; i++)
{
adjList[i] = new LinkedList();
}
}

// Method to create an edge into the graph
// from node x to y and y to x
void addingEdge(int x, int y)
{
// The Graph is not directed
adjList[x].add(y);
adjList[y].add(x); 
}


// A method that finds the chromatic number of a graph
void findChromticNo(int arr[])
{
// caculating the size of the array
int size = arr.length;
Set<Integer> hashSet = new HashSet<Integer>();

// iterating over every node and  
// storing its color in the hashset
for(int j = 0; j < size; j++)
{
// hashset only contains unique numbers.
hashSet.add(arr[j]);
}

// finding the chromatic Number of the graph
int chromaticNo = hashSet.size();

System.out.println("The chromatic number of the graph is: " + chromaticNo);

}

// Assigning colors (beginning from 0) to all the nodes and
// displaying the assignment of colors
void greedyColorNodes()
{
int res[] = new int[N];

// Initializing all the vertices as unassigned
Arrays.fill(res, -1);

// Assiging the first color to the first vertex
res[0] = 0;

// A temporary array in order to keep the available colors. A False
// value of the avail[clr] will mean that the color clr has been assigned
// to one of its adjacent nodes
boolean avail[] = new boolean[N];

// In the beginning, all of the colors are available
Arrays.fill(avail, true);

// Assign colors to theh remaining N - 1 nodes
for (int n = 1; n < N; n++)
{
// Processing all the adjacent nodes and flag their colors as unavailable
Iterator<Integer> itr = adjList[n].iterator() ;
while (itr.hasNext())
{
int i = itr.next();
if (res[i] != -1)
	avail[res[i]] = false;
}

// Find the first color that is available
int clr;
for (clr = 0; clr < N; clr++)
{
if (avail[clr])
{
break;
}
}

res[n] = clr; // Assigning the found color

// For the next iteration, resetting the values back to true 
Arrays.fill(avail, true);
}

// printing the result
for (int n = 0; n < N; n++)
{
System.out.println("Node " + n + " ---> Color - " + res[n]);
}
// for finding the chromatic number of the graph
findChromticNo(res);
}
// main method
public static void main(String argvs[])
{
// creating a graph that contains 
// 5 nodes
Graphs graph1 = new Graphs(5);

// creating edges between nodes
graph1.addingEdge(0, 1);
graph1.addingEdge(0, 2);
graph1.addingEdge(1, 2);
graph1.addingEdge(1, 3);
graph1.addingEdge(2, 3);
graph1.addingEdge(3, 4);

System.out.println("Coloring of the graph 1 is: ");

// invoking the method greedyColorNodes() to color the nodes
graph1.greedyColorNodes();

System.out.println();

// creating a graph that contains 
// 4 nodes
Graphs graph2 = new Graphs(4);

System.out.println("Coloring of the graph 2 is: ");

// creating edges between nodes
graph2.addingEdge(0, 1);
graph2.addingEdge(0, 2);
graph2.addingEdge(1, 3);
graph2.addingEdge(2, 3);

// invoking the method greedyColorNodes() to color the nodes
graph2.greedyColorNodes();


}

}

Output:

Coloring of the graph 1 is: 
Node 0 ---> Color - 0
Node 1 ---> Color - 1
Node 2 ---> Color - 2
Node 3 ---> Color - 0
Node 4 ---> Color - 1
The chromatic number of the graph is: 3

Coloring of the graph 2 is: 
Node 0 ---> Color - 0
Node 1 ---> Color - 1
Node 2 ---> Color - 1
Node 3 ---> Color - 0
The chromatic number of the graph is: 2

Let's see the graph, we have used in the above program.

Graph-1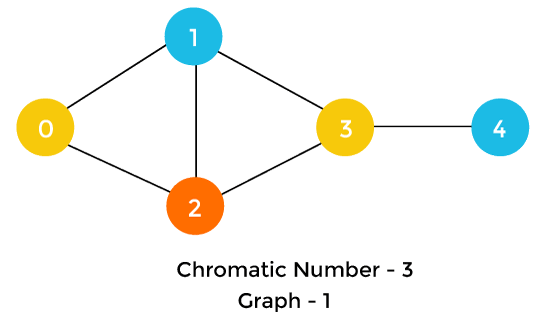

Graph-2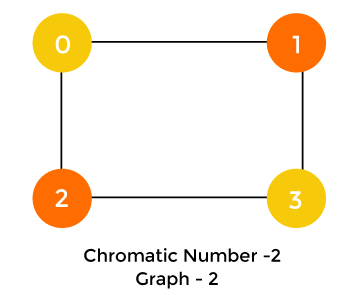

Application of Chromatic Number

There is a lot of applications where chromatic number is used. A few of them are mentioned below.

1) Assignment of Mobile Radio Frequency: At the same location, when frequencies are being assigned to mobile towers, there must be the difference in the frequencies assigned to all the towers. To assign the frequencies with this constraint, and the number of frequencies should also be the minimum, we need the help of chromatic numbers. The towers can be treated as nodes, and an edge between these two nodes shows the towers are in the range of each other. Now, this is the standard graph coloring problem, where we have to reduce the total number of unique colors, which is given by the chromatic number of the graph.

2) Time Table or Making Schedule: Suppose, one has to create an exam schedule for a college or university. The person has the information about all the subjects, and the students enrolled in them. A simple way of scheduling is to conduct exam of only one subject in a one-time slot. Thus, the total time slot will be equal to the total number of subjects available. However, such kind of scheduling is not efficient, as it is required to minimize the time slots.

Also, one cannot schedule the exam of all subjects in a single time slot. It is because one student may get enrolled in different subjects. If the exam is happening of those subjects in a single time slot, then the student can only give exam of the single subject, rest of other exams is going to be missed by the student.

Thus, the time slots have to be minimized in such a way that there is no conflict. To do so, we take the graph coloring technique. The subjects are treated as nodes, and an edge will only exist between two nodes if there is a common student that is enrolled to those two subjects. After creating the graph, find its chromatic number. The chromatic number gives the minimum time slots required to conduct the exam successfully.

Next TopicSublime Number in Java

← prev next →