Practical Number in Java

In this section, we will learn what is a practical number and also create Java programs to check if the given number is a practical number or not. The practical number program is frequently asked in Java coding interviews and academics.

Practical Number

A number X is said to be the practical number in Java if all the numbers Y that are less than X (Y < X) should be written as the addition of a unique proper divisor of X. Note that the proper divisor of a number excludes that number itself.

Steps to Find the Practical Numbers

Step 1: Assign a number to the variable.

Step 2: Find the proper divisors of the given number.

Step 3: Store these divisors in a list.

Step 4: Take all the numbers that are less than the given number (1 to given number - 1), one by one and try to find the subset from the list (found in step 3) whose sum is equal to the taken number.

Step 5: Check whether subsets are found or not for every number from 1 to given number - 1. If the subsets are found, then the given number is the practical number; otherwise, not.

Examples of Practical Number

Given, X = 10

Then, proper divisors of X are: 1, 2, 5

All the numbers that are less than 10 are Y = {1, 2, 3, 4, 5, 6, 7, 8, 9}

Check whether every number present in Y or not.

1 = 1 (1 is the proper divisor of X)

2 = 2 (2 is also the proper divisor of X)

3 = 1 + 2 (1 & 2 both are proper divisors of X. Also, they are unique)

4 = 2 + 2 (2 is the proper divisor of X. However, 2 has come twice, which is not unique)

Hence, we found at least one number which does not satisfy the stated condition. Therefore, the number 10 is not a practical number.

Given, X = 12

Then, proper divisors of X are: 1, 2, 3, 4, 6

All the numbers that are less than 12 are Y = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}

Check whether every number present in Y or not.

1 = 1 (1 is the proper divisor of X)

2 = 2 (2 is also the proper divisor of X)

3 = 1 + 2 (1 & 2 both are proper divisors of X. Also, they are unique)

4 = 1 + 3 (1 & 3 both are proper divisors of X. Also, they are unique)

5 = 2 + 3 (2 & 3 both are proper divisors of X. Also, they are unique)

6 = 2 + 4 (2 & 4 both are proper divisors of X. Also, they are unique)

7 = 3 + 4 (3 & 4 both are proper divisors of X. Also, they are unique)

8 = 2 + 6 (2 & 6 both are proper divisors of X. Also, they are unique)

9 = 3 + 6 (3 & 6 both are proper divisors of X. Also, they are unique)

10 = 1 + 3 + 6 (1, 3, & 6 both are proper divisors of X. Also, they are unique)

11 = 2 + 3 + 6 (2, 3 & 6 all are proper divisors of X. Also, they are unique)

Hence, we found that all the numbers present in Y satisfy the given condition. Therefore, the number 12 is a practical number.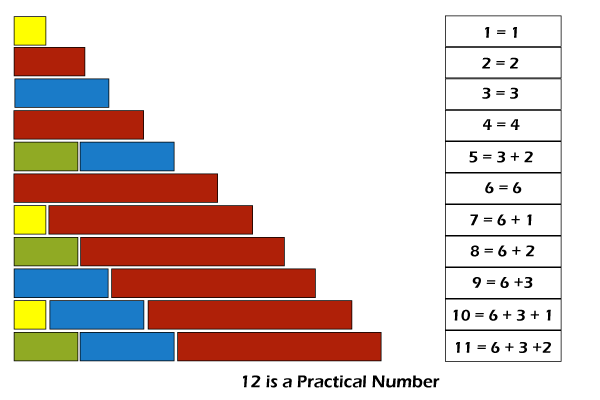

Practical Number Java Program

Observe the following Java program that checks the practical numbers from 1 to 20.

FileName: PracticalNumberExample.java

// Import Statement
import java.util.*;

public class PracticalNumberExample
{
// A method that returns true whenever s is equal to the sum of a subset of v
public boolean isSumSubset(int s, int size, Vector<Integer> v)
{
// The value of isSubset[j][i] will give true, when
// there is a subset of v[0..i-1] with the sum
// equal to j 
boolean isSubset[][] = new boolean[size + 1][s + 1];

// the answer is true whenever we get the sum as 0
for (int j = 0; j <= size; j++)
{
isSubset[j][0] = true;
}

// the subset is not empty and the sum is 0. Hence, the false value
for (int j = 1; j <= s; j++)
{
isSubset[0][j] = false;
}

// Filling the subset table in the bottom-up manner
for (int j = 1; j <= size; j++)
{
for (int i = 1; i <= s; i++)
{
if (i < v.get(j - 1))
{
isSubset[j][i] = isSubset[j - 1][i];
}
if (i >= v.get(j - 1))
{
isSubset[j][i] = isSubset[j - 1][i] || isSubset[j - 1][i - v.get(j - 1)];
}
}
}
return isSubset[size][s];
}

// a method to keep all the divisors of no in the vector f
public void keepDivisors(int no, Vector<Integer> f)
{
// A loop that looks for all divisors that divides 'num'
for (int j = 1; j <= Math.sqrt(no); j++)
{

// if 'j' is the divisor of 'no'
if (no % j == 0)
{

// if divisor and quotient both are same 
// then either divisor or quotient will be considered
// for example - 9 / 3 = 3. In this case, quotient and 
// divisor both are 3. Hence, only one 3 will be stored in the vector f
if (j == (no / j))
f.add(j);
else
{
f.add(j);
f.add(no / j);
}
}
}
}

// A method that returns true whenever num is a practical number
public boolean isPracticalNo(int num)
{
// a vector for storing all the factors of num
Vector<Integer> factor = new Vector<Integer>();

// a method that fills the vector factor
keepDivisors(num, factor);
int size = factor.size();

// to check all numbers from 1 to < num
for (int j = 1; j < num; j++)
{
if (!isSumSubset(j, size, factor))
return false;
}
return true;
}

// main method
public static void main(String argvs[])
{
// creating an object of the class PracticalNumberExample
PracticalNumberExample pNumObj = new PracticalNumberExample(); 


for(int i = 1; i <= 20; i++)
{
if(pNumObj.isPracticalNo(i) == true)
System.out.println("The number " + i + " is the practical number.");
else
System.out.println("The number " + i + " is not the practical number.");
}
}
}

Output:

The number 1 is the practical number.
The number 2 is the practical number.
The number 3 is not the practical number.
The number 4 is the practical number.
The number 5 is not the practical number.
The number 6 is the practical number.
The number 7 is not the practical number.
The number 8 is the practical number.
The number 9 is not the practical number.
The number 10 is not the practical number.
The number 11 is not the practical number.
The number 12 is the practical number.
The number 13 is not the practical number.
The number 14 is not the practical number.
The number 15 is not the practical number.
The number 16 is the practical number.
The number 17 is not the practical number.
The number 18 is the practical number.
The number 19 is not the practical number.
The number 20 is the practical number.

Explanation: For every number from 1 to 20, the method isPracticalNo() is invoked with the help of for-loop. For every number, a vector factor is created for storing its divisors. Now, for every number from 1 to the given number (num), we try to find the subset with the help of dynamic programming. If for every number from 1 to the given number (num) we find a subset, then the given number (num) is the perfect number; otherwise, not.