Counting sort in JavaCounting sort is one of the most used sorting techniques in Java that is based on the keys b/w specific range. Counting sort doesn't perform sorting by comparing elements. It performs sorting by counting objects having distinct key values like hashing. After that, it performs some arithmetic operations for calculating the index position of each object in the output sequence. The counting sort algorithm is not used as a general-purpose sorting algorithm. Suppose, we have an input array a{4, 3, 2, 5, 4, 3, 5, 1, 0, 2, 5} which have values in the range[0, 5]. 
We count the occurrence of each element in the array and represent the countings as an array countArray. The countArray[i] represents the occurrence of the number i in the array a. 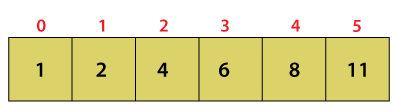
So, number 0 and 1 appear one time, 2, 3, and 4 appears two times and 5 appear three times. 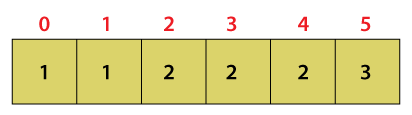
Now, with the help of the countArray, we determine how many elements are less than or equal to each element of the countArray in array a. We sum all the elements which are less than or equal to countArray[i]. In array a,
AlgorithmAfter getting the auxiliary array, i.e., countArray, we perform sorting to sort the array a. These are the following steps to sort the elements of the array a.
So, in order to sort the input array a, we iterate it in reverse order and start with the number 5. At index 5 in the countArray, we have value 11, which means array 'a' contains 11 elements that are less or equal to the number 5. It means 5 will be our last element in the sorted array. 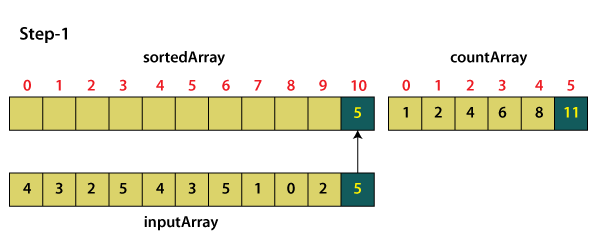
After moving number 5 in the sorted array, we decrement the value of countArray[5]. Now, the next number in the reverse order is 2, and at index 2, we have value 4, which means array 'a' contains four elements that are less than or equal to 2. So, the number will be at position 4 in the sorted array. 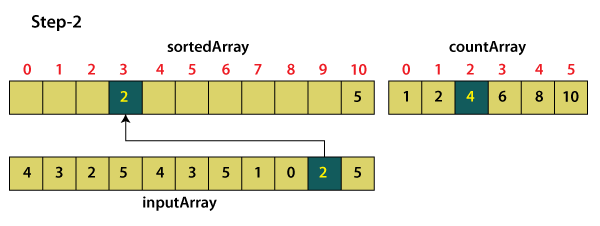
The next number is 0 in the input array 'a' and the value in the countArray at index 0 is 1 which means there is only one element in the input array 'a', which is equal to 0. So, 0 will be the first element in the sorted array. 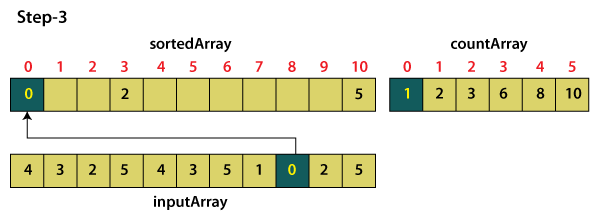
We perform the same operation for the remaining elements of the input array 'a'. For element 1 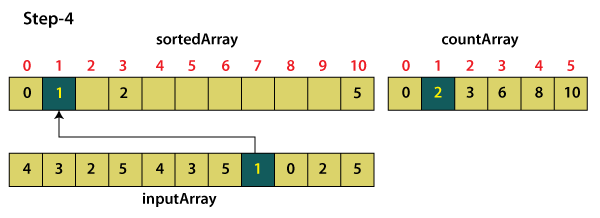
For element 5 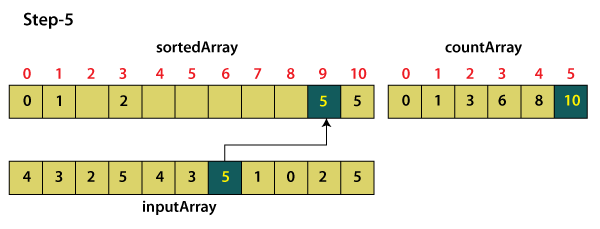
For element 3 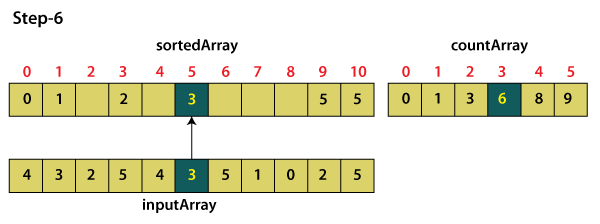
For element 4 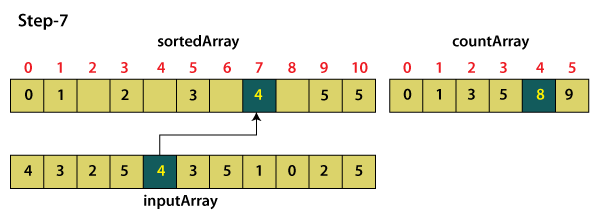
For element 5 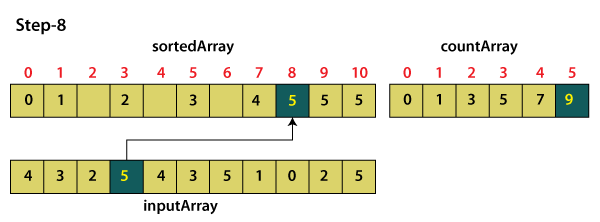
For element 2 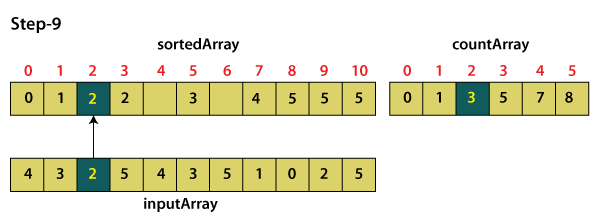
For element 3 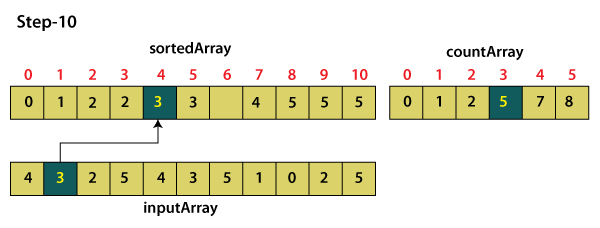
For element 4 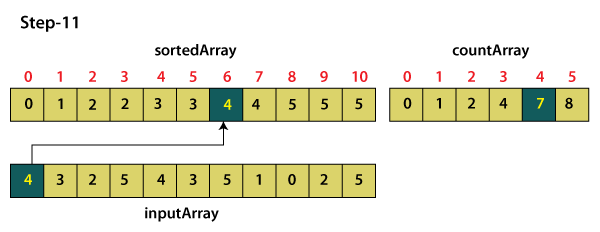
Sorted Array 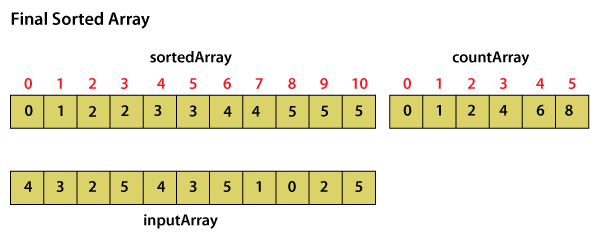
Let's implement the logic of the counting sort in Java by using the above-discussed algorithm: CountingSortExample.java Output: 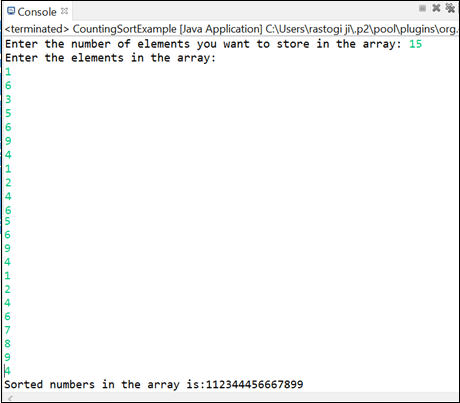
Next TopicCRC Program in Java
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










