Diffie-Hellman Algorithm in Java

Diffie-Hellman algorithm is one of the most important algorithms used for establishing a shared secret. At the time of exchanging data over a public network, we can use the shared secret for secret communication. We use an elliptic curve for generating points and getting a secret key using the parameters.

We will take four variables, i.e., P (prime), G (the primitive root of P), and a and b (private values).
The variables P and G both are publicly available. The sender selects a private value, either a or b, for generating a key to exchange publicly. The receiver receives the key, and that generates a secret key, after which the sender and receiver both have the same secret key to encrypt.

Let's understand the process step by step for user1 (sender) and user2 (receiver):

Steps	User1	User2
1.	P, G => available public keys.	P, G => available public keys.
2.	a is selected as a private key.	b is selected as a private key.
3.	Eq. to generate key: x=G^a modP	Eq. to generate key: y=G^b modP
4.	After exchanging keys, user1 receives key y.	After exchanging keys, user2 receives key x.
5.	User1 generates a secret key by using the received key y: k_a=y^a modP	User2 generates a secret key by using the received key x: k_b=x^b modP

Algebraically, 5^th step can be shown as follows:

k_a=k_b

It means that both the users have the symmetric secret key to encrypt.

Example:

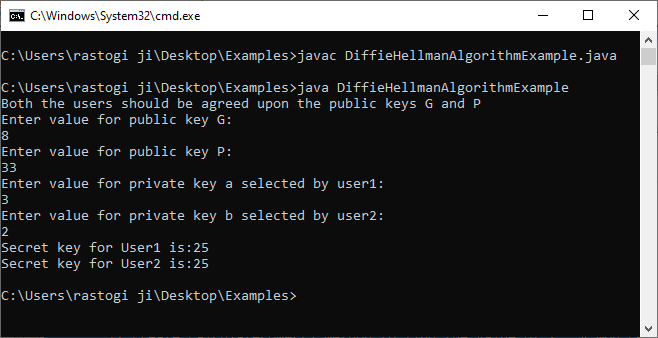
User1 and User2 get public keys P = 33 and G = 8.
User1 selects a as a private key, i.e., 3, and User2 selects b as a private key, i.e., 2.
User1 calculate the public value:
x=(8³ mod 33)=512mod33=17
User2 calculate the public value:
y=(8² mod33)=64mod33= 31
User1 and User2 exchange public keys, i.e., 17 and 31.
User1 receives public key y = 31 and User2 receives public key x = 17.
User1 and User2 calculate symmetric keys:
User1: k_a=y_a modP=31₃ mod33=29791mod33=25
User2:k_b=x_b modP=17₂ mod33=289mod33=25
25 is the shared secret.

Now, let's implement the Java code for the Diffie-Hellman algorithm:

DiffieHellmanAlgorithmExample.java

import java.util.*;
// create class DiffieHellmanAlgorithmExample to calculate the key for two persons
class DiffieHellmanAlgorithmExample {
    // main() method start
    public static void main(String[] args)
    {
        long P, G, x, a, y, b, ka, kb;
        // create Scanner class object to take input from user
        Scanner sc = new Scanner(System.in);
        System.out.println("Both the users should be agreed upon the public keys G and P");
        // take inputs for public keys from the user
        System.out.println("Enter value for public key G:");
        G = sc.nextLong();
        System.out.println("Enter value for public key P:");
        P = sc.nextLong();
        // get input from user for private keys a and b selected by User1 and User2
        System.out.println("Enter value for private key a selected by user1:");
        a = sc.nextLong();
        System.out.println("Enter value for private key b selected by user2:");
        b = sc.nextLong();
        
        // call calculatePower() method to generate x and y keys
        x = calculatePower(G, a, P);
        y = calculatePower(G, b, P);
        // call calculatePower() method to generate ka and kb secret keys after the exchange of x and y keys        
        // calculate secret key for User1
        ka = calculatePower(y, a, P);
        // calculate secret key for User2 
        kb = calculatePower(x, b, P);
        // print secret keys of user1 and user2
        System.out.println("Secret key for User1 is:" + ka);
        System.out.println("Secret key for User2 is:" + kb);
    }
    // create calculatePower() method to find the value of x ^ y mod P
    private static long calculatePower(long x, long y, long P)
    {
        long result = 0;        
        if (y == 1){
            return x;
        }
        else{
            result = ((long)Math.pow(x, y)) % P;
            return result;
        }
    }	
}

Output: