Minimum Cost Path Problem in Java

The minimum cost path problem in Java is one the most prominent problems that have been asked in the interview. In this problem, a matrix is provided (costMatrix[][]), which represents the cost of each of the cells present in the costMatrix[][]. The task is to go from the top left corner to the bottom right corner such that the cost is minimum. We have to return the minimum cost. The rule from going from one cell to another cell is that one can only go in the left or down or the diagonal direction, with one cell at a time. For example, from the current cell, say costMatrix[x][y], we can only go to one of these cells: costMatrix[x][y + 1] (the left direction), costMatrix[x + 1][y] (the downward direction), and costMatrix[x + 1][y + 1] (the diagonal direction).

For example, in the following matrix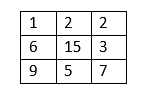

There are the following paths to go from the top-left cell (of the cost 1) to the bottom-right cell (of the cost 7).

1 -> 6 -> 9 -> 5 -> 7		Total Cost = 1 + 6 + 9 + 5 + 7 = 28
1 -> 6 -> 15 -> 5 -> 7		Total Cost = 1 + 6 + 15 + 5 + 7 = 34
1 -> 6 -> 15 -> 3 -> 7		Total Cost = 1 + 6 + 15 + 3 + 7 = 32
1 -> 6 -> 15 -> 7		Total Cost = 1 + 6 + 15 + 7 = 29
1 -> 6 -> 5 -> 7		Total Cost = 1 + 6 + 5 + 7 = 19
1 -> 2 -> 15 -> 3 -> 7		Total Cost = 1 + 2 + 15 + 3 + 7 = 28
1 -> 2 -> 15 -> 5 -> 7		Total Cost = 1 + 2 + 15 + 5 + 7 = 30
1 -> 2 -> 15 -> 7		Total Cost = 1 + 2 + 15 + 7 = 25
1 -> 2 -> 2 -> 3 -> 7		Total Cost = 1 + 2 + 2 + 3 + 7 = 15
1 -> 2 -> 3 -> 7		Total Cost = 1 + 2 + 3 + 7 = 13

In all the above-mentioned paths, the last path (1 -> 2 -> 3 -> 7, total cost: 13) has the minimum cost. Therefore, 13 is the required answer of the above matrix.

Note: It is assumed that cost of any cell of the matrix is always non-negative.

Approach

There are two approaches to solve this problem: one is recursive, and the other is iterative (using dynamic programming). Let's start with the recursive approach.

Implementation: Recursive

The recursive approach is also the brute force approach. In this approach, we will explore all the paths and, in those paths, we will select the minimum cost path. Observe the following program.

FileName: MinCostPath.java

public class MinCostPath
{
// a method that finds the minimum among 
// the numbers a, b, and c
public int min(int a, int b, int c)
{
if(a < b)
{
if(a < c)
{
return a;
}
else
{
return c;
}
}

else
{
if(b < c)
{
return b;
}
else
{
return c;
}

}
}
public int minCostPath(int costMatrix[][], int i, int j, int row, int col)
{
// the i index exceeds the total number of rows
// present in the matrix. Hence, we need to return
if(i >= row)
{
return Integer.MAX_VALUE;
}

// the j index exceeds the total number of columns
// present in the matrix. Hence, we need to return
else if(j >= col)
{
return Integer.MAX_VALUE;
}

// the bottom right cell has been reached
if(i == row - 1 && j == col - 1)
{
return costMatrix[i][j];
}

// recursively going in the left, downward, and the diagonal direction
return costMatrix[i][j] + min(minCostPath(costMatrix, i + 1, j, row, col),
minCostPath(costMatrix, i, j + 1, row, col),
minCostPath(costMatrix, i + 1, j + 1, row, col));

}

// main method
public static void main(String argvs[])
{
//creating an object of the class MinCostPath
MinCostPath obj = new MinCostPath();

// input array
int costMatrix[][] = { {1, 2, 2},
{6, 15, 3},
{9, 5, 7} };

// row length of the matrix          
int row = costMatrix.length;

// column length of the matrix
int col = costMatrix[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix[i][j] + " ");
}
System.out.println();
}


int ans = obj.minCostPath(costMatrix, 0, 0, row, col);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 

System.out.println();

// input array
int costMatrix1[][] = { {10, 12, 20},
{16, 5, 13},
{19, 50, 17} };

// row length of the matrix          
row = costMatrix1.length;

// column length of the matrix
col = costMatrix1[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix1[i][j] + " ");
}
System.out.println();
}


ans = obj.minCostPath(costMatrix1, 0, 0, row, col);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 




}
}

Output:

For the following matrix: 
1 2 2 
6 15 3 
9 5 7 

The minimum cost path from the top-left to the bottom-right is: 13

For the following matrix: 
10 12 20 
16 5 13 
19 50 17 

The minimum cost path from the top-left to the bottom-right is: 32

Complexity Analysis: In the above program, one recursive call gives rise to the three recursive calls. Thus, the time complexity of the above program is exponential. Exponential time complexity is large and should be avoided when one deals with a large amount of data. Therefore, one should do the optimization to reduce the time complexity.

If we observe the above program, we will find that there are many sub-problems that have been computed more than one time, leading to the exponential time complexity. Observe the following.

// first recursive call
minCostPath(0, 0) -> minCostPath(1, 0) & minCostPath(0, 1) & minCostPath(1, 1)

// second recursive call
minCostPath(1, 0) -> minCostPath(2, 0) & minCostPath(1, 1), & minCostPath(2, 1)

We see that minCostPath(1, 1) is coming more than once. Therefore, we have to compute the value of minCostPath(1, 1) more than once. If we further extend the recursive calls, we will find that there are many recursive calls that are redundant and that should be avoided. The following program shows how one can avoid the repetition of the recursive calls. It uses the recursion with memoization technique.

FileName: MinCostPath1.java

public class MinCostPath1
{
// a method that finds the minimum among 
// the numbers a, b, and c
public int min(int a, int b, int c)
{
if(a < b)
{
if(a < c)
{
return a;
}
else
{
return c;
}
}

else
{
if(b < c)
{
return b;
}
else
{
return c;
}

}
}
public int minCostPath(int costMatrix[][], int i, int j, int row, int col, int remVal[][])
{

// the i index exceeds the total number of rows
// present in the matrix. Hence, we need to return
if(i >= row)
{
return Integer.MAX_VALUE;
}

// the j index exceeds the total number of columns
// present in the matrix. Hence, we need to return
else if(j >= col)
{
return Integer.MAX_VALUE;
}


// if remVal[i][j] != -1
// then it means we have already visited
// the cell[i][j] and from there we have
// alraedy computed the value of minimum cost till the 
// bottom-right element
if(remVal[i][j] != -1)
{
return remVal[i][j];
}

// the bottom right cell has been reached
if(i == row - 1 && j == col - 1)
{
return costMatrix[i][j];
}

// recursively going in the left, downward, and the diagonal direction
remVal[i][j] = costMatrix[i][j] + min(minCostPath(costMatrix, i + 1, j, row, col, remVal),
minCostPath(costMatrix, i, j + 1, row, col, remVal),
minCostPath(costMatrix, i + 1, j + 1, row, col, remVal));

return remVal[i][j];

}

// main method
public static void main(String argvs[])
{
//creating an object of the class MinCostPath1
MinCostPath1 obj = new MinCostPath1();

// input array
int costMatrix[][] = { {1, 2, 2},
{6, 15, 3},
{9, 5, 7} };

// row length of the matrix          
int row = costMatrix.length;

// column length of the matrix
int col = costMatrix[0].length;

int remVal[][] = new int[row][col];

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
// initializing the elements of the matrix remVal with -1
remVal[i][j] = -1;
}
}

System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix[i][j] + " ");

// initializing the elements of the matrix remVal with -1
remVal[i][j] = -1;
}
System.out.println();
}


int ans = obj.minCostPath(costMatrix, 0, 0, row, col, remVal);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 


System.out.println();

// input array
int costMatrix1[][] = { {10, 12, 20},
{16, 5, 13},
{19, 50, 17} };

// row length of the matrix          
row = costMatrix1.length;

// column length of the matrix
col = costMatrix1[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix1[i][j] + " ");
}
System.out.println();
}

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
// initializing the elements of the matrix remVal with -1
remVal[i][j] = -1;
}
}

ans = obj.minCostPath(costMatrix1, 0, 0, row, col, remVal);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 


}
}

Output:

For the following matrix: 
1 2 2 
6 15 3 
9 5 7 

The minimum cost path from the top-left to the bottom-right is: 13

For the following matrix: 
10 12 20 
16 5 13 
19 50 17 

The minimum cost path from the top-left to the bottom-right is: 32

Complexity Analysis: In the above program also, one recursive call give rise to the three recursive calls. However, not every recursive call will go till the end. Since we have avoided the computation of the repetitive subproblem; therefore, the time complexity of the above program is around O(row * column), where row and column are the row size and column size of the cost matrix, which comes at the cost of some extra space. The extra space used is of the order O(row * column).

Implementation: Iterative

In this approach, we will be using dynamic programming to solve the minimum cost path problem. Observe the following program.

FileName: MinCostPath2.java

public class MinCostPath2
{
// a method that finds the minimum among 
// the numbers a, b, and c
public int min(int a, int b, int c)
{
if(a < b)
{
if(a < c)
{
return a;
}
else
{
return c;
}
}

else
{
if(b < c)
{
return b;
}
else
{
return c;
}

}
}


public int minCostPath(int costMatrix[][], int row, int col)
{
int i;
int j;
int totalCost[][] = new int[row][col];

totalCost[0][0] = costMatrix[0][0];

// Initializing the first column of the totalCost array
for (j = 1; j < row; j++)
{
    totalCost[j][0] = totalCost[j - 1][0] + costMatrix[j][0];
    
}

// Initializing the first row of the totalCost 
for (i = 1; i < col; i++)
{
    totalCost[0][i] = totalCost[0][i - 1] + costMatrix[0][i];
   
}

// Constructing the rest of the totalCost array
for (j = 1; j < row; j++)
{
    for (i = 1; i < col; i++)
    {
        totalCost[j][i] = min(totalCost[j - 1][i - 1],
                       totalCost[j - 1][i],
                       totalCost[j][i - 1]) + costMatrix[j][i];
    }


}

return totalCost[row - 1][col - 1];
}






// main method
public static void main(String argvs[])
{
//creating an object of the class MinCostPath2
MinCostPath2 obj = new MinCostPath2();

// input array
int costMatrix[][] = { {1, 2, 2},
{6, 15, 3},
{9, 5, 7} };

// row length of the matrix          
int row = costMatrix.length;

// column length of the matrix
int col = costMatrix[0].length;

System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix[i][j] + " ");

}
System.out.println();
}


int ans = obj.minCostPath(costMatrix, row, col);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 


System.out.println();

// input array
int costMatrix1[][] = { {10, 12, 20},
{16, 5, 13},
{19, 50, 17} };

// row length of the matrix          
row = costMatrix1.length;

// column length of the matrix
col = costMatrix1[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix1[i][j] + " ");
}
System.out.println();
}



ans = obj.minCostPath(costMatrix1, row, col);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 


}

}

Output:

For the following matrix: 
1 2 2 
6 15 3 
9 5 7 

The minimum cost path from the top-left to the bottom-right is: 13

For the following matrix: 
10 12 20 
16 5 13 
19 50 17 

The minimum cost path from the top-left to the bottom-right is: 32

Complexity Analysis: In the above program, there are many single for-loop. However, there is also a nested for-loops of degree two. Therefore, the time complexity of the above program is O(row * column), where the row is the total number of rows present in the input array and the column is the column size of the input array. Also, the program is using some extra space (a 2-dimensional array: totalCost[][]), which makes the space complexity of the program O(row * column).

Note that if the interviewer allows that it is allowed to modify the input array, then we can discard the 2-dimensional array (totalCost[][]) to reduce the space complexity of the above program to O(1). The time complexity of the program remains the same. The following program shows the same.

FileName: MinCostPath3.java

public class MinCostPath3
{
// a method that finds the minimum among 
// the numbers a, b, and c
public int min(int a, int b, int c)
{
if(a < b)
{
if(a < c)
{
return a;
}
else
{
return c;
}
}

else
{
if(b < c)
{
return b;
}
else
{
return c;
}

}
}


public int minCostPath(int costMatrix[][], int row, int col)
{
int i;
int j;


// Initializing the first column of the totalCost array
for (j = 1; j < row; j++)
{
    costMatrix[j][0] = costMatrix[j - 1][0] + costMatrix[j][0];
    
}

// Initializing the first row of the totalCost 
for (i = 1; i < col; i++)
{
    costMatrix[0][i] = costMatrix[0][i - 1] + costMatrix[0][i];
   
}

// Constructing the rest of the totalCost array
for (j = 1; j < row; j++)
{
    for (i = 1; i < col; i++)
    {
        costMatrix[j][i] = min(costMatrix[j - 1][i - 1],
                       costMatrix[j - 1][i],
                       costMatrix[j][i - 1]) + costMatrix[j][i];
    }


}

return costMatrix[row - 1][col - 1];
}






// main method
public static void main(String argvs[])
{
//creating an object of the class MinCostPath3
MinCostPath3 obj = new MinCostPath3();

// input array
int costMatrix[][] = { {1, 2, 2},
{6, 15, 3},
{9, 5, 7} };

// row length of the matrix          
int row = costMatrix.length;

// column length of the matrix
int col = costMatrix[0].length;

System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix[i][j] + " ");

}
System.out.println();
}


int ans = obj.minCostPath(costMatrix, row, col);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 


System.out.println();

// input array
int costMatrix1[][] = { {10, 12, 20},
{16, 5, 13},
{19, 50, 17} };

// row length of the matrix          
row = costMatrix1.length;

// column length of the matrix
col = costMatrix1[0].length;


System.out.println("For the following matrix: ");

for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
System.out.print(costMatrix1[i][j] + " ");
}
System.out.println();
}



ans = obj.minCostPath(costMatrix1, row, col);
System.out.println();
System.out.println("The minimum cost path from the top-left to the bottom-right is: " + ans); 


}

}

Output:

For the following matrix: 
1 2 2 
6 15 3 
9 5 7 

The minimum cost path from the top-left to the bottom-right is: 13

For the following matrix: 
10 12 20 
16 5 13 
19 50 17 

The minimum cost path from the top-left to the bottom-right is: 32

Next TopicDiffie-Hellman Algorithm in Java

← prev next →