Dutch National Flag Problem in Java | Java Program to Short an Array of 0's, 1's, and 2's

Dutch National Flag (DNF) problem is one of the most popular programming problems proposed by the famous Dutch computer scientist Edsger Dijkstra. As its name suggest, it is based on the flag of Netherlands that consists tri colors i.e. red, white, and blue. The task is to randomly arrange the bolls of red, white, and blue in such a way that balls of the same color are placed together.

We will solve the above problem using an array. Instead of using the colors, here we will use 0's, 1's, and 2's that represents red, white, and blue colors, respectively. In order to match the color of the bolls we will sort the array.

For example, consider the following array.

Input: {0, 1, 2, 2, 1, 0, 0, 2, 0, 1, 1, 0}

Output: {0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2}

So, Dutch National flag problem is the same as short an array of 0's, 1's, and 2's. In this section, we will create a Java program for the same.

Solution to the Problem

There are many solutions are available that may vary in performance and characteristics.

Naive Approach

The simple solution is to perform the counting sort over the array. In this sorting, we count the frequency of the elements (0, 1, and 2), after that put them in the correct order. The disadvantage of the approach is that it traverses two times over the array, one for sorting, second for putting elements in the correct order.

In order to overcome the above shortcoming, we reorganize the array in such a way that solves the problem in single traversal. It uses an alternative linear-time partition routine (the same as 3-way partition) that separates the values into the following three groups.

The values (red) less than the pivot.
The values (white) equal to the pivot, and
The values (blue) greater than the pivot.

Algorithm

	procedure three-way-partition(A : array of values, mid : value):
    i ← 0
    j ← 0
    k ← size of A - 1
    while j <= k:
        if A[j] < mid:
            swap A[i] and A[j]
            i ← i + 1
            j ← j + 1
        else if A[j] > mid:
            swap A[j] and A[k]
            k ← k - 1
        else:
            j ← j + 1

Let's understand it through an example.

Example

In the following example, we have used three variables low, mid, and high. The low and mid pointer point at start and the high pointer point at the end of the array. There are three cases:

If array[mid]=0, swap array[mid] with array[low] and increment both the pointers by one.
If array[mid]=1, no swapping performed but increment the mid pointer.
If array[mid]=2, swap array[mid] with array[high] and decrement the high pointer by one.

Consider the following array.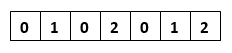

Initially low and mid points the start of the array i.e. 0 and the high points end of the array i.e. 2.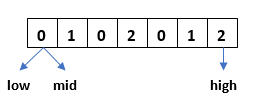

Step 1: Check if array[mid]=0, swap array[mid] with array[low] and increment both the pointers by 1.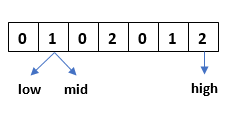

Step 2: Check if array[mid]=1, no swapping is required. Increment the mid pointer by 1.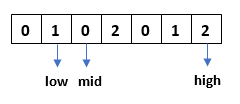

Step 3: Check if array[mid]=0, swap array[mid] with array[low] and increment both the pointers by 1.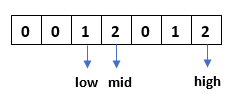

Step 4: Check if array[mid]=2, swap array[mid] with array[high] and decrement the high pointer by 1.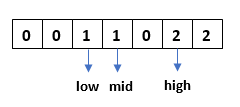

Step 5: Check if array[mid]=1, no swapping required increments the pointers by 1.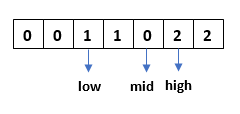

Step 6: Check if array[mid]=0, swap array[mid] with array[low] and increment both the pointers by 1.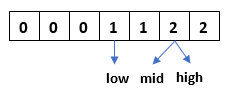

Step 7: Check if array[mid]=2, swap array[mid] with array[high] and decrement the high pointer by 1.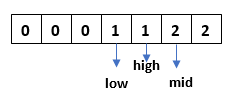

We overserve that the array is sorted.

Let's implement the above approach in Java programs with different logics.

Dutch National Flag Problem Java Program

DutchNationalFlag.java

import java.util.Arrays;
public class DutchNationalFlag
{
    // Linear time partition routine to sort an array containing 0, 1, and 2.
    // It is similar to 3-way partitioning for the Dutch national flag problem.
    public static void threeWayPartition(int[] A)
    {
        int start = 0, mid = 0;
        int pivot = 1;
        int end = A.length - 1;
        while (mid <= end)
        {
            if (A[mid] < pivot)         // if current element is 0
            {
                swap(A, start, mid);
                ++start;
                ++mid;
            }
            else if (A[mid] > pivot)    // if current element is 2
            {
                swap(A, mid, end);
                --end;
            }
            else {                      // if current element is 1
                ++mid;
            }
        }
    } 
    // Utility function to swap elements `A[i]` and `A[j]` in the array
    private static void swap(int[] A, int i, int j)
    {
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }
//driver code
    public static void main (String args[])
    {
	//array to be short
        int[] A = { 0, 1, 2, 2, 1, 0, 0, 2, 0, 1, 1, 0 };
 
        threeWayPartition(A);
	//prints sorted array 
        System.out.println(Arrays.toString(A));
    }
}

Output:

[0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2]

Let's see another logic for the same.

DutchFlagProblem.java

import java.io.*; 
public class DutchFlagProblem 
{ 
	static void DNFS(int arr[], int arr_size) 
	{ 
		int low = 0; 
		int high = arr_size - 1; 
		int mid = 0, temp=0; // temp variable is used for swapping 
		while (mid <= high) 
		{ 
			switch (arr[mid]) 
			{ 
        case 0: // if mid pointer points at 0
        { 
        //swapping logic    
          temp = arr[low]; 
          arr[low] = arr[mid]; 
          arr[mid] = temp; 
          low++; 
          mid++; 
          break; 
        } 
        case 1: // if mid pointer points at 1
        //no swapping required only increment the mid pointer
          mid++; 
          break; 
        case 2: // if mid pointer points at 2
        { 
        //swapping logic    
          temp = arr[mid]; 
          arr[mid] = arr[high]; 
          arr[high] = temp; 
          high--; 
          break; 
        } 
			} 
		} 
	} 
	//function to print array sorted and unsorted array 
	static void printArray(int arr[], int arr_size) 
	{ 
		int i; 
		//loop iterate over the array
		for (i = 0; i < arr_size; i++) 
		//prints array elements 
			System.out.print(arr[i]+" "); 
			//prints space
		System.out.println(""); 
	} 
	/*Driver function to check for above functions*/
	public static void main (String args[]) 
	{ 
		int arr[] = {0, 0, 1, 2, 0, 1, 2}; 
		//finds length of the array
		int arr_size = arr.length; 
    System.out.println("Array before Sorting: "); 
		printArray(arr, arr_size); 
		//function calling before sorting
    DNFS(arr, arr_size); 
    //printing sorted array
    System.out.println("Array after sorting: "); 
    //function calling after sorting
		printArray(arr, arr_size); 
	} 
}

Output:

Array before Sorting: 
0 0 1 2 0 1 2 
Array after sorting: 
0 0 0 1 1 2 2

The above program shorts the array in linear time without using extra space. The array is traversed only once. Hence, the time complexity of the is O(n), where n is the size of the array.

Next TopicJava Calculate Average of List

← prev next →