Hamming Code in JavaHamming code is a special code in a Computer network, which is a set of error-correction codes. In Computer Graphics, it is mainly used for detecting and correcting errors that occur at the time of data transmission from sender to receiver. In Java, we can implement the code to detect and correct errors using Hamming code. The code is known as Hamming code because it was developed by R.W. Hamming to detect and correct errors. The redundant bits and parity bits play an important role in detecting and correcting errors. Redundant bits are the extra binary bits that are added to the original data bits, which are ready to transfer from sender to receiver for ensuring that no bits were lost during the data transfer. Parity bits are the extra bits that are added to the original data(binary bits) so that the total number of 1s is even or odd. To learn more about Hamming code, redundant bits, and parity bits, go through the section. General Hamming Code AlgorithmWe use the parity bits for identifying and correcting errors, and the process of using parity bits for identifying the error is referred to as Hamming code. These are the following steps for Hamming code:

Let's implement the logic for Hamming code in Java by taking reference to the above steps: HammingCodeExample.java Output: 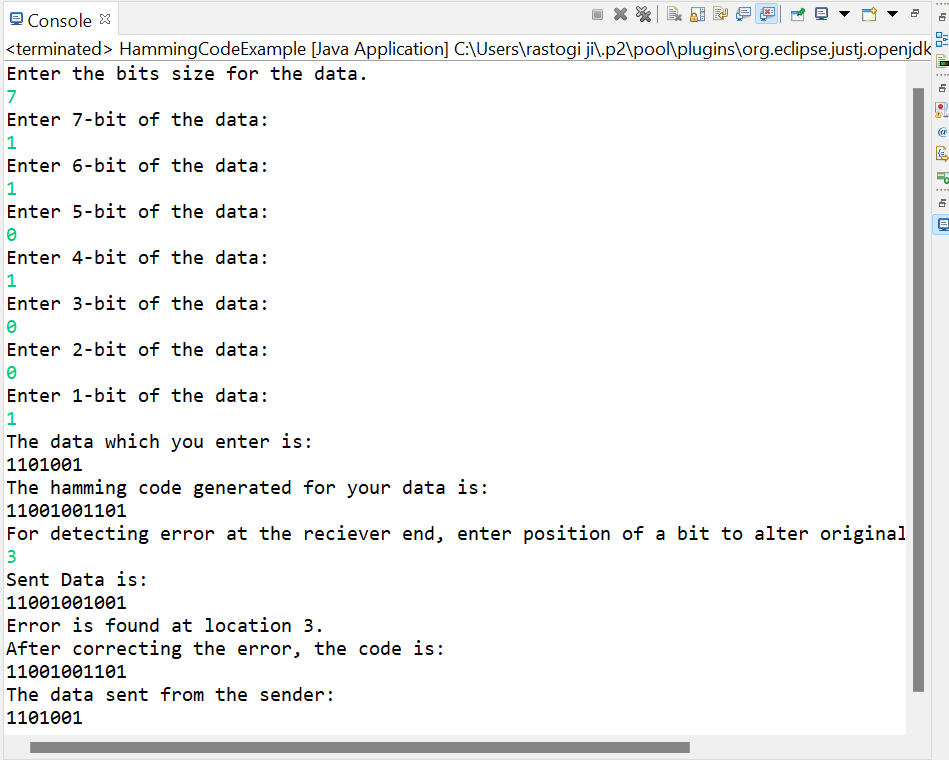
Next TopicMap of Map in Java
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










