Error CorrectionError Correction codes are used to detect and correct the errors when data is transmitted from the sender to the receiver. Error Correction can be handled in two ways:
A single additional bit can detect the error, but cannot correct it. For correcting the errors, one has to know the exact position of the error. For example, If we want to calculate a single-bit error, the error correction code will determine which one of seven bits is in error. To achieve this, we have to add some additional redundant bits. Suppose r is the number of redundant bits and d is the total number of the data bits. The number of redundant bits r can be calculated by using the formula: 2r>=d+r+1 The value of r is calculated by using the above formula. For example, if the value of d is 4, then the possible smallest value that satisfies the above relation would be 3. To determine the position of the bit which is in error, a technique developed by R.W Hamming is Hamming code which can be applied to any length of the data unit and uses the relationship between data units and redundant units. Hamming CodeParity bits: The bit which is appended to the original data of binary bits so that the total number of 1s is even or odd. Even parity: To check for even parity, if the total number of 1s is even, then the value of the parity bit is 0. If the total number of 1s occurrences is odd, then the value of the parity bit is 1. Odd Parity: To check for odd parity, if the total number of 1s is even, then the value of parity bit is 1. If the total number of 1s is odd, then the value of parity bit is 0. Algorithm of Hamming code:
Relationship b/w Error position & binary number.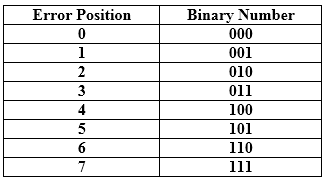
Let's understand the concept of Hamming code through an example: Suppose the original data is 1010 which is to be sent.
Total number of data bits 'd' = 4
Number of redundant bits r : 2r >= d+r+1
2r>= 4+r+1
Therefore, the value of r is 3 that satisfies the above relation.
Total number of bits = d+r = 4+3 = 7;
Determining the position of the redundant bitsThe number of redundant bits is 3. The three bits are represented by r1, r2, r4. The position of the redundant bits is calculated with corresponds to the raised power of 2. Therefore, their corresponding positions are 1, 21, 22. Representation of Data on the addition of parity bits: 
Determining the Parity bitsDetermining the r1 bitThe r1 bit is calculated by performing a parity check on the bit positions whose binary representation includes 1 in the first position. 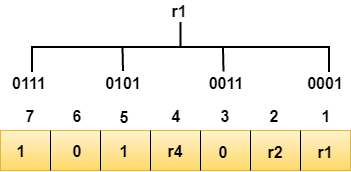
We observe from the above figure that the bit positions that includes 1 in the first position are 1, 3, 5, 7. Now, we perform the even-parity check at these bit positions. The total number of 1 at these bit positions corresponding to r1 is even, therefore, the value of the r1 bit is 0. Determining r2 bitThe r2 bit is calculated by performing a parity check on the bit positions whose binary representation includes 1 in the second position. 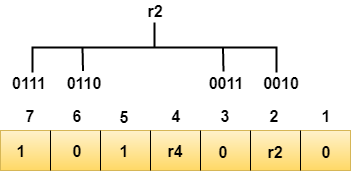
We observe from the above figure that the bit positions that includes 1 in the second position are 2, 3, 6, 7. Now, we perform the even-parity check at these bit positions. The total number of 1 at these bit positions corresponding to r2 is odd, therefore, the value of the r2 bit is 1. Determining r4 bitThe r4 bit is calculated by performing a parity check on the bit positions whose binary representation includes 1 in the third position. 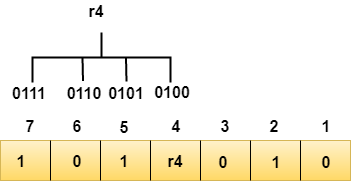
We observe from the above figure that the bit positions that includes 1 in the third position are 4, 5, 6, 7. Now, we perform the even-parity check at these bit positions. The total number of 1 at these bit positions corresponding to r4 is even, therefore, the value of the r4 bit is 0. Data transferred is given below: 
Suppose the 4th bit is changed from 0 to 1 at the receiving end, then parity bits are recalculated. R1 bitThe bit positions of the r1 bit are 1,3,5,7 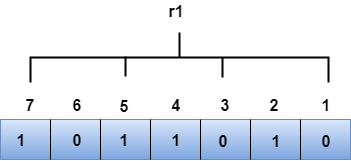
We observe from the above figure that the binary representation of r1 is 1100. Now, we perform the even-parity check, the total number of 1s appearing in the r1 bit is an even number. Therefore, the value of r1 is 0. R2 bitThe bit positions of r2 bit are 2,3,6,7. 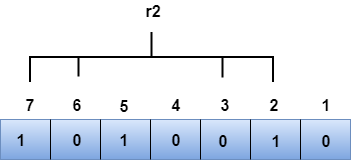
We observe from the above figure that the binary representation of r2 is 1001. Now, we perform the even-parity check, the total number of 1s appearing in the r2 bit is an even number. Therefore, the value of r2 is 0. R4 bitThe bit positions of r4 bit are 4,5,6,7. 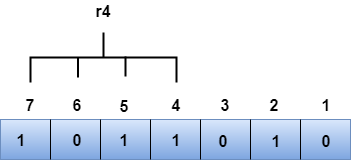
We observe from the above figure that the binary representation of r4 is 1011. Now, we perform the even-parity check, the total number of 1s appearing in the r4 bit is an odd number. Therefore, the value of r4 is 1.
Next Topic#
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










