Noisy and Noiseless Channel

What is a Noise?

DEFINITION: Noise refers to any undesirable signal that corrupts or distorts the originally transmitted message in a communication system. Various factors, such as electromagnetic interference, thermal agitation, or electrical cross-talk can cause it. The presence of noise in a transmission channel reduces the quality and reliability of the received signal, making it more difficult for the receiver to decode the original message accurately. To combat the effects of noise, engineers often employ techniques such as error correction coding, signal amplification, and filtering to minimize its impact and ensure the integrity of the transmitted data.

The signal may be distorted by a variety of noise forms, including thermal noise, generated noise, crosstalk, and impulsive noise. The random movement of electrons in a wire, known as thermal noise, results in an additional signal that was not initially sent by the transmitter. The transmission medium serves as the receiving antenna, and these devices serve as the transmitting antenna. The impact of one wire on another is known as crosstalk. The transmission antenna is one wire, while the receiving antenna is the other. Impulse noise is a spike that is caused by electrical lines, lightning, and other sources that produce signals with great energy in a brief period of time. The provided figure illustrates how noise affects a signal.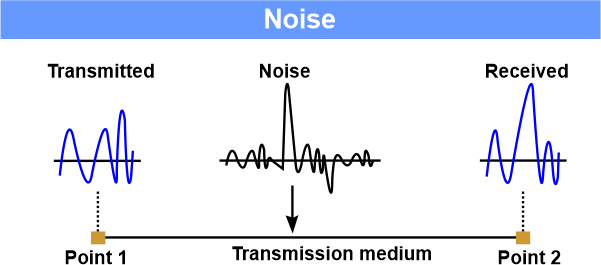

Signal-to-Noise Ratio

In a communication system, the signal-to-noise ratio is an important factor in determining the reliability and accuracy of the transmitted information. The goal is to maximize the signal-to-noise ratio so that the receiver can accurately decode the original message with minimal error. Improving the signal-to-noise ratio can be achieved by reducing the noise or increasing the signal strength, or by using error correction coding or signal processing techniques to filter out the noise.

The formula of the signal-to-noise ratio is:

We must take into account the average signal and noise powers because they could alter over time. The idea of SNR is depicted in the accompanying figure.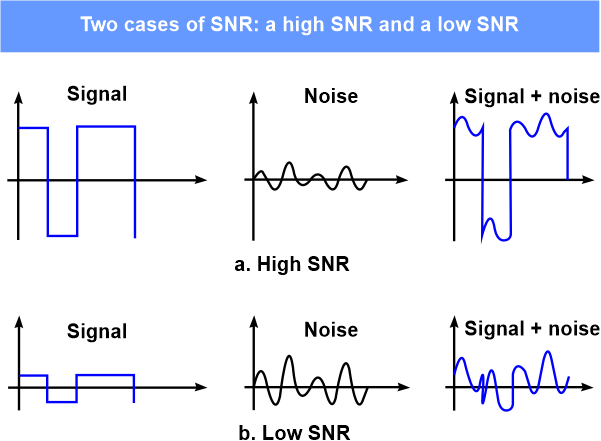

Signal-to-noise ratio (SNR) is a measure of the relative strength of a desired signal to the level of unwanted background noise in a communication system. It is expressed as the ratio of the power of the signal to the power of the noise, and is typically measured in decibels (dB). A higher signal-to-noise ratio indicates a stronger signal compared to the noise, and therefore, better signal quality and a clearer transmission.

SNR_dB is defined as follows:

SNRdB = 10Log10SNR

How to calculate Data Rate in any channel?

The data rate in a channel can be calculated by considering the amount of information that is transmitted over the channel in a given amount of time. The formula for data rate, also known as bandwidth, is given by:

Data Rate (R) = Total number of bits transmitted / Total time taken to transmit the bits

The total number of bits transmitted can be calculated by multiplying the number of symbols transmitted per second by the number of bits per symbol. For example, suppose a channel uses quadrature amplitude modulation (QAM). In that case, the number of bits per symbol can be calculated based on the number of possible combinations of amplitude and phase levels. It's important to note that the data rate is also influenced by various other factors, such as the frequency spectrum available for transmission, the type of modulation used, and the amount of noise present in the channel. To maximize the data rate, it is often necessary to optimize the transmission scheme, use error correction coding, and employ techniques to reduce the effects of noise.

There are several factors that can affect the data rate in a communication channel. Here are three key ones:

• Channel Capacity: The channel capacity, or the maximum data rate that can be transmitted over a channel, is limited by various physical and electrical constraints, such as the bandwidth of the channel, the amount of noise present, and the type of modulation used.
• Modulation Technique: Different modulation techniques can transmit data over a channel. For example, amplitude modulation (AM) and frequency modulation (FM) has limited data rates. In contrast, more advanced techniques like quadrature amplitude modulation (QAM) and orthogonal frequency-division multiplexing (OFDM) can support higher data rates.
• Interference and Noise: Interference from other sources and background noise in the channel can have a significant impact on the data rate. These factors can cause degradation in the quality of the signal, making it more difficult for the receiver to accurately decode the information. To combat the effects of noise, engineers often employ techniques such as error correction coding, signal amplification, and filtering to minimize its impact and ensure the integrity of the transmitted data.

Two formulas were developed, one by Nyquist and one by Shannon, to calculate the data rate in communication channels. The formula by Nyquist is designed for noise-free channels, while the formula by Shannon takes into account the presence of noise in the channel.

Noiseless Channel - Nyquist Bit Rate

A noiseless channel is a communication system in which the signal transmitted from the sender to the receiver is free from any unwanted background noise or interference. In other words, a noiseless channel is a theoretical ideal where the signal quality is perfect and the information transmitted is not degraded by any extraneous factors.

This type of channel is often used as a reference in communications theory and engineering to understand the effects of noise on the data rate and signal quality. A noiseless channel is an idealized concept and does not exist in reality, as all communication channels are inherently subject to some form of noise or interference. However, by employing techniques such as error correction coding, signal processing, and channel equalization, it is possible to minimize the effects of noise and improve the signal quality in real-world communication systems.

The theoretical maximum bit rate for a noiseless channel is determined by the Nyquist bit rate formula:

BitRate = 2 x bandwidth x Log2L

The equation mentioned uses three terms, bandwidth, L (representing the number of signal levels used for data representation), and BitRate (the rate at which bits are transmitted in bits per second). According to the equation, increasing the number of signal levels could result in a higher bit rate. However, this is only true in theory. In practice, there is a limit to how many signal levels can be utilized before the receiver becomes too complex and the system becomes unreliable.

For example, when the signal only has two levels, the receiver can easily distinguish between a 0 and a 1. But as the number of signal levels increases, the receiver must be increasingly sophisticated to discriminate between them, making the system less reliable. This trade-off highlights the practical limitations of using the equation to achieve higher bit rates in real-world communication systems.

Here one question arises:

Does the bit rate predicted by the Nyquist theorem match the intuitive bit rate mentioned in baseband transmission?

Answer - The bit rate predicted by the Nyquist theorem and the intuitive bit rate in baseband transmission may or may not match, depending on the specific communication system being considered.

The Nyquist theorem provides a theoretical upper limit for the bit rate in a noiseless channel based on the bandwidth and signal-to-noise ratio. The intuitive bit rate in baseband transmission is a rough estimate of the data rate that can be achieved in a real-world communication system, taking into account practical limitations such as noise and interference.

In a noiseless channel, the bit rate predicted by the Nyquist theorem should match the intuitive bit rate in baseband transmission. However, in a noisy channel, the bit rate predicted by the Nyquist theorem will be lower than the intuitive bit rate in baseband transmission due to the effects of noise and interference on the signal quality.

In summary, the match between the bit rate predicted by the Nyquist theorem and the intuitive bit rate in baseband transmission will depend on the specific communication system being considered and the level of noise and interference in the channel.

Noisy Channel - Shannon Capacity

A noisy channel is a communication system in which the transmission of data is impaired by external interference or internal degradation of the signal. This interference, known as noise, can take many forms, including thermal noise, electromagnetic interference, and crosstalk.

SHANNON CAPACITY - Shannon capacity, also known as channel capacity, is a concept in information theory introduced by Claude E. Shannon in 1948. It represents the maximum amount of information that can be transmitted through a communication channel per unit of time, given the channel's characteristics and constraints. The channel capacity is expressed in bits per second (bps). It is determined by the channel's bandwidth, signal-to-noise ratio, and the type of signaling used (e.g., binary or multi-level).

The channel capacity provides a theoretical upper limit for the data rate that can be achieved over a given communication channel. It is important to note that this limit is a theoretical ideal and does not take into account the practical limitations of real-world communication systems, such as noise, interference, and errors. Despite these limitations, the channel capacity remains a valuable tool for designing and analyzing communication systems, as it provides a benchmark for comparing the performance of different channels and transmission techniques.

In practice, there is no such thing as a noiseless channel; noise is always present. The Shannon capacity is given as:

Capacity = bandwidth x Log2(1 + SNR)

The Shannon capacity calculation takes into account the channel's bandwidth, signal-to-noise ratio, and bit-per-second capacity. Unlike the number of signal levels, this formula does not include the signal level, so the channel's capacity cannot be exceeded. The formula represents a property of the channel rather than a transmission technique.

Consider a channel that is incredibly noisy and has a signal-to-noise ratio of almost 0. Or to put it another way, the signal is weak because of the noise. The formula used to determine this channel's capacity C is?

Ans.

Capacity, C = B log₂(1 + SNR)

= B log₂(1 + 0)

= B log₂1

= B x 0

= 0

As a result, this channel has no ability to transmit data, regardless of its bandwidth. In other words, it lacks the capability to carry any information.