Cristian's Algorithm

Client processes synchronise time with a time server using Cristian's Algorithm, a clock synchronisation algorithm. While redundancy-prone distributed systems and applications do not work well with this algorithm, low-latency networks where round trip time is short relative to accuracy do. The time interval between the beginning of a Request and the conclusion of the corresponding Response is referred to as Round Trip Time in this context.

An example mimicking the operation of Cristian's algorithm is provided below: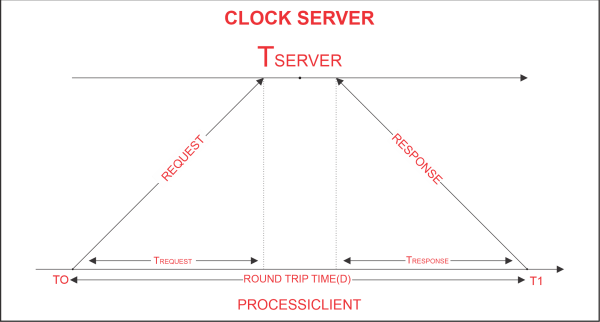

Algorithm:

The process on the client machine sends the clock server a request at time T 0 for the clock time (time at the server).
In response to the client process's request, the clock server listens and responds with clock server time.
The client process retrieves the response from the clock server at time T₁ and uses the formula below to determine the synchronised client clock time.

T_CLIENT = T_SERVER plus (T₁ - T₀)/2.

where T_CLIENT denotes the synchronised clock time, T_SERVER denotes the clock time returned by the server, T₀ denotes the time at which the client process sent the request, and T₁ denotes the time at which the client process received the response

The formula above is valid and reliable:

Assuming that the network latency T₀ and T₁ are roughly equal, T₁ - T₀ denotes the total amount of time required by the network and server to transfer the request to the server, process it, and return the result to the client process.

The difference between client-side and real-time time is no more than (T₁ - T₀)/2 seconds. We can infer from the aforementioned statement that the synchronisation error can only be (T₁ - T₀)/2 seconds at most.

Hence,

Error E [-(T 1 - T 0)/2, (T 1 - T 0)/2]

The Python codes below demonstrate how Cristian's algorithm functions.

To start a clock server prototype on a local machine, enter the following code:

Python

# Python3 program imitating a clock server

import socket
import datetime

# function used to initiate the Clock Server
def initiateClockServer():

	s = socket.socket()
	print("Socket successfully created")
	
	# Server port
	port = 8000

	s.bind(('', port))
	
	# Start listening to requests
	s.listen(5)	
	print("Socket is listening...")
	
	# Clock Server Running forever
	while True:
	
	# Establish connection with client
	connection, address = s.accept()	
	print('Server connected to', address)
	
	# Respond the client with server clock time
	connection.send(str(
					datetime.datetime.now()).encode())
	
	# Close the connection with the client process
	connection.close()


# Driver function
if __name__ == '__main__':

	# Trigger the Clock Server
	initiateClockServer()

Output:

Socket successfully created
Socket is listening...

On the local machine, the following code runs a client process prototype:

Python

# Python3 program imitating a client process

import socket
import datetime
from dateutil import parser
from timeit import default_timer as timer

# function used to Synchronize client process time
def synchronizeTime():

	s = socket.socket()		
	
	# Server port
	port = 8000	
	
	# connect to the clock server on local computer
	s.connect(('127.0.0.1', port))

	request_time = timer()

	# receive data from the server
	server_time = parser.parse(s.recv(1024).decode())
	response_time = timer()
	actual_time = datetime.datetime.now()

	print("Time returned by server: " + str(server_time))

	process_delay_latency = response_time - request_time

	print("Process Delay latency: " \
		+ str(process_delay_latency) \
		+ " seconds")

	print("Actual clock time at client side: " \
		+ str(actual_time))

	# synchronize process client clock time
	client_time = server_time \
					+ datetime.timedelta(seconds = \
							(process_delay_latency) / 2)

	print("Synchronized process client time: " \
										+ str(client_time))

	# calculate synchronization error
	error = actual_time - client_time
	print("Synchronization error : "
				+ str(error.total_seconds()) + " seconds")

	s.close()	


# Driver function
if __name__ == '__main__':

	# synchronize time using clock server
	synchronizeTime()

Output:

Time returned by server: 2018-11-07 17:56:43.302379
Process Delay latency: 0.0005150819997652434 seconds
Actual clock time at client side: 2018-11-07 17:56:43.302756
Synchronized process client time: 2018-11-07 17:56:43.302637
Synchronization error : 0.000119 seconds

We can define a minimum transfer time that we can use to create an improved synchronisation clock time through iterative testing over the network (less synchronisation error).

The server time will always be generated after T₀ + T min in this case, and T_SERVER will always be generated before T₁ - T_min, where T min is the minimum transfer time, which is the minimum value of T_REQUEST and T_RESPONSE during several iterative tests. Here, a formulation of the synchronisation error is as follows:

Error E [-((T₁ - T₀)/2-T_min), ((T₁ - T₀)/2-T_min)]

Similar to this, if T_REQUEST and T_RESPONSE differ by a significant amount of time, T_MIN1 and T_MIN2 may be used in place of T_MIN1 and T_MIN2, respectively, where T_MIN1 denotes the minimum observed request time and T_MIN2 denotes the minimum observed response time over the network.

In this scenario, the synchronised clock time can be calculated as follows:

(T₁ - T₀)/2 + (T_min2 - T_min1)/2 +T_SERVER = T_CLIENT

Therefore, we can improve clock time synchronisation and subsequently reduce the overall synchronisation error by simply introducing response and request time as separate time latencies. The total clock drift that is seen will determine how many iterative tests need to be performed.

Next TopicService Set Identifier (SSID) in Computer Network

← prev next →