Parzen Windows density Estimation Technique

Density estimation plays a vital function in statistical analysis and device getting to know. It entails estimating the underlying chance density function (PDF) from a given set of facts. Parzen Windows, also referred to as kernel density estimation, is a popular and flexible non-parametric technique used for estimating chance densities. In this article, we delve into the idea of Parzen Windows and explore its packages, advantages, and obstacles.

Understanding Parzen Windows:

Parzen Windows is a technique that estimates the PDF by means of placing a window (regularly a Gaussian kernel) round each information point and summing up the contributions from all of the windows. The width or bandwidth of the window determines the smoothness of the estimated density. The name "Parzen Windows" is derived from the work of Emanuel Parzen, who introduced this technique in the Sixties.

Mathematically, the Parzen Windows density estimator is described as follows:

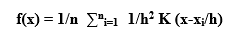
where:

• f(x) is the estimated PDF at point x
• n is the number of data points.
• h is the width or bandwidth of the window.
• d is the dimensionality with the ith data point.
• xi represents the ith data point.
• K (.) is the kernel function, often a symmetric function such as the Gaussian kernel.

Applications of Parzen Windows:

1. Density Estimation: Parzen Windows offer a flexible way to estimate the underlying chance density feature of a given dataset without making any assumptions about its distribution. It is especially useful while dealing with small or irregularly allotted datasets.
2. Outlier Detection: By estimating the density at every point, Parzen Windows can discover regions of low density, making it effective for outlier detection. Data factors that lie in regions with substantially decreased density can be taken into consideration as ability outliers.
3. Pattern Recognition: Parzen Windows can be used in sample recognition tasks, consisting of character reputation or photo segmentation. By estimating the densities of different lessons, it will become feasible to classify new instances based totally on their likelihoods.

Limitations and Challenges:

1. Computational Complexity: As the quantity of fact points will increase, the computation of the density estimation can become computationally steeply-priced, especially in excessive-dimensional spaces.
2. Bandwidth Selection: Choosing the suitable bandwidth is critical for correct density estimation. A bandwidth that is too big can over smooth the density, whilst a bandwidth that is too small can lead to overfitting and noise amplification.
3. Curse of Dimensionality: Parzen Windows suffer from the curse of dimensionality. As the dimensionality of the facts increases, the specified amount of statistics to acquire accurate density estimation grows exponentially.

Advantages of Parzen Windows:

1. Non-parametric: Parzen Windows no longer makes assumptions about the underlying distribution of the statistics. They can estimate densities for any form of dataset, making them rather bendy and applicable in a huge variety of eventualities.
2. Adaptability: The preference of kernel function in Parzen Windows lets in for adaptability to exclusive records traits. Different kernel features can be used based on the shape and homes of the information distribution, enabling customization and improved accuracy in density estimation.
3. Control over smoothness: The bandwidth parameter in Parzen Windows lets in for manage over the smoothness of the estimated density. A large bandwidth produces a smoother estimate that may assist in shooting standard traits and lowering noise. On the opposite hand, a smaller bandwidth captures extra detailed variations and local systems inside the facts.
4. Outlier detection: Parzen Windows may be used for outlier detection by way of identifying regions of low density. Data factors that lie in areas with notably decreased density than the encircling areas may be taken into consideration as potential outliers.

Disadvantages of Parzen Windows:

1. omputational complexity: As the variety of statistics points will increase, the computational complexity of Parzen Windows grows substantially. For every information point, a kernel wishes to be evaluated for all different information points, resulting in a time complexity of O(n^2) for a dataset with n points. This can be computationally expensive, especially in high-dimensional areas or with large datasets.
2. Bandwidth choice: Choosing the precise bandwidth is vital for correct density estimation with Parzen Windows. However, determining the top-quality bandwidth is not a trivial project and may be hard. A bandwidth that is too huge can over smooth the density and fail to capture neighborhood versions, even as a bandwidth that is too small can result in overfitting and noise amplification.
3. Curse of dimensionality: Parzen Windows be afflicted by the curse of dimensionality. As the dimensionality of the information will increase, the amount of information required to gain correct density estimation grows exponentially. This is due to the fact the facts will become sparser in high-dimensional areas, making it tough to estimate densities correctly.
4. Boundary consequences: Parzen Windows are influenced by means of the boundaries of the facts. The kernel home windows close to the rims of the dataset might not fully capture the density because of factors falling out of doors the variety of the kernel. This can cause biased density estimates near the limits of the records.