Distance Vector Routing Algorithm
- The Distance vector algorithm is iterative, asynchronous and distributed.
- Distributed: It is distributed in that each node receives information from one or more of its directly attached neighbors, performs calculation and then distributes the result back to its neighbors.
- Iterative: It is iterative in that its process continues until no more information is available to be exchanged between neighbors.
- Asynchronous: It does not require that all of its nodes operate in the lock step with each other.
- The Distance vector algorithm is a dynamic algorithm.
- It is mainly used in ARPANET, and RIP.
- Each router maintains a distance table known as Vector.
Three Keys to understand the working of Distance Vector Routing Algorithm:
- Knowledge about the whole network: Each router shares its knowledge through the entire network. The Router sends its collected knowledge about the network to its neighbors.
- Routing only to neighbors: The router sends its knowledge about the network to only those routers which have direct links. The router sends whatever it has about the network through the ports. The information is received by the router and uses the information to update its own routing table.
- Information sharing at regular intervals: Within 30 seconds, the router sends the information to the neighboring routers.
Distance Vector Routing Algorithm
Let dx(y) be the cost of the least-cost path from node x to node y. The least costs are related by Bellman-Ford equation,
dx(y) = minv{c(x,v) + dv(y)}
Where the minv is the equation taken for all x neighbors. After traveling from x to v, if we consider the least-cost path from v to y, the path cost will be c(x,v)+dv(y). The least cost from x to y is the minimum of c(x,v)+dv(y) taken over all neighbors.
With the Distance Vector Routing algorithm, the node x contains the following routing information:
- For each neighbor v, the cost c(x,v) is the path cost from x to directly attached neighbor, v.
- The distance vector x, i.e., Dx = [ Dx(y) : y in N ], containing its cost to all destinations, y, in N.
- The distance vector of each of its neighbors, i.e., Dv = [ Dv(y) : y in N ] for each neighbor v of x.
Distance vector routing is an asynchronous algorithm in which node x sends the copy of its distance vector to all its neighbors. When node x receives the new distance vector from one of its neighboring vector, v, it saves the distance vector of v and uses the Bellman-Ford equation to update its own distance vector. The equation is given below:
dx(y) = minv{ c(x,v) + dv(y)} for each node y in N
The node x has updated its own distance vector table by using the above equation and sends its updated table to all its neighbors so that they can update their own distance vectors.
Algorithm
At each node x,
Initialization
for all destinations y in N:
Dx(y) = c(x,y) // If y is not a neighbor then c(x,y) = ∞
for each neighbor w
Dw(y) = ? for all destination y in N.
for each neighbor w
send distance vector Dx = [ Dx(y) : y in N ] to w
loop
wait(until I receive any distance vector from some neighbor w)
for each y in N:
Dx(y) = minv{c(x,v)+Dv(y)}
If Dx(y) is changed for any destination y
Send distance vector Dx = [ Dx(y) : y in N ] to all neighbors
forever
Note: In Distance vector algorithm, node x update its table when it either see any cost change in one directly linked nodes or receives any vector update from some neighbor.
Let's understand through an example:
Sharing Information
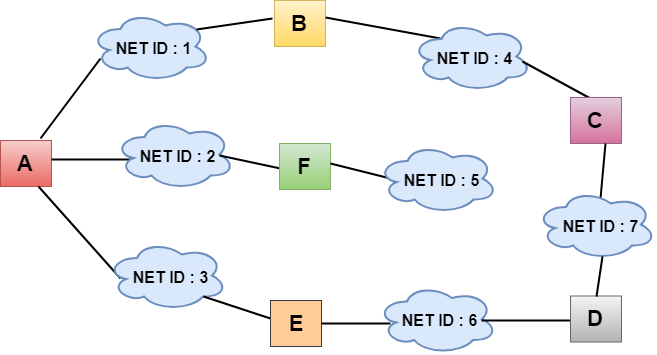
- In the above figure, each cloud represents the network, and the number inside the cloud represents the network ID.
- All the LANs are connected by routers, and they are represented in boxes labeled as A, B, C, D, E, F.
- Distance vector routing algorithm simplifies the routing process by assuming the cost of every link is one unit. Therefore, the efficiency of transmission can be measured by the number of links to reach the destination.
- In Distance vector routing, the cost is based on hop count.
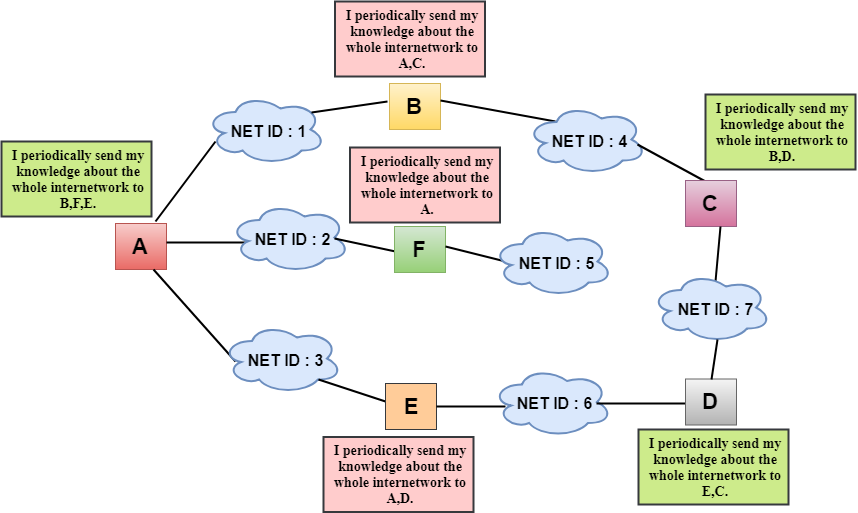
In the above figure, we observe that the router sends the knowledge to the immediate neighbors. The neighbors add this knowledge to their own knowledge and sends the updated table to their own neighbors. In this way, routers get its own information plus the new information about the neighbors.
Routing Table
Two process occurs:
- Creating the Table
- Updating the Table
Creating the Table
Initially, the routing table is created for each router that contains atleast three types of information such as Network ID, the cost and the next hop.
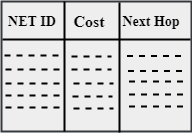
- NET ID: The Network ID defines the final destination of the packet.
- Cost: The cost is the number of hops that packet must take to get there.
- Next hop: It is the router to which the packet must be delivered.
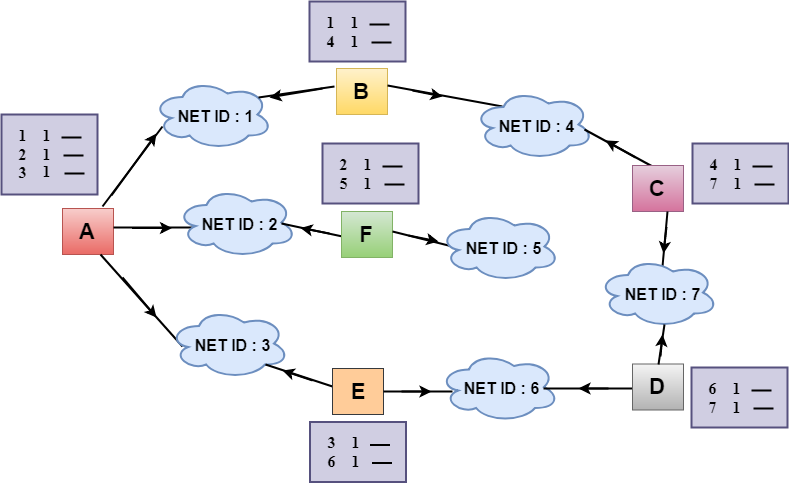
- In the above figure, the original routing tables are shown of all the routers. In a routing table, the first column represents the network ID, the second column represents the cost of the link, and the third column is empty.
- These routing tables are sent to all the neighbors.
For Example:
Updating the Table
- When A receives a routing table from B, then it uses its information to update the table.
- The routing table of B shows how the packets can move to the networks 1 and 4.
- The B is a neighbor to the A router, the packets from A to B can reach in one hop. So, 1 is added to all the costs given in the B's table and the sum will be the cost to reach a particular network.

- After adjustment, A then combines this table with its own table to create a combined table.
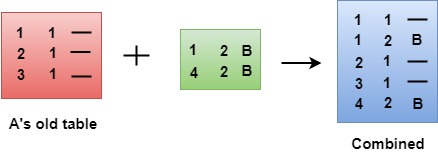
- The combined table may contain some duplicate data. In the above figure, the combined table of router A contains the duplicate data, so it keeps only those data which has the lowest cost. For example, A can send the data to network 1 in two ways. The first, which uses no next router, so it costs one hop. The second requires two hops (A to B, then B to Network 1). The first option has the lowest cost, therefore it is kept and the second one is dropped.
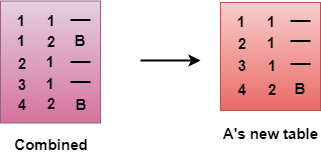
- The process of creating the routing table continues for all routers. Every router receives the information from the neighbors, and update the routing table.
Final routing tables of all the routers are given below:
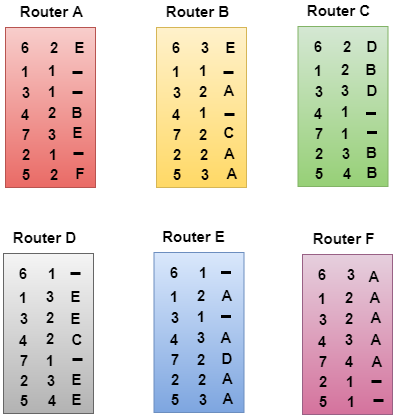
|








 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now










