Count to Infinity Problem in Distance Vector Routing

Since the Bellman-Ford algorithm is unable to prevent loops, the fundamental problem with Distance Vector Routing (DVR) protocols is Routing Loops. The Count to Infinity Problem is brought on by this routing loop in the DVR network. When two routers deliver updates simultaneously or when an interface goes down, routing loops frequently happen.

Count to Infinity:

Distance-vector routing has the drawback that while cost increases (bad news) propagate slowly, cost decreases (positive news) propagate quickly. Distance-vector routing takes some time for all other routers to become aware of a broken connection (cost becomes infinity), which is necessary for a routing protocol to function properly. Counting to infinity is the name given to the issue. A broken link's cost may not always be registered as infinite by all routers until numerous updates have passed.

Two Node Loop:

The two-node loop issue is an example of count to infinity. Let's examine the case shown in Figure to better grasp the issue.

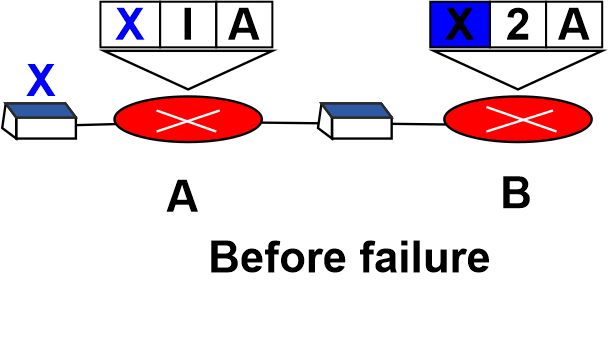
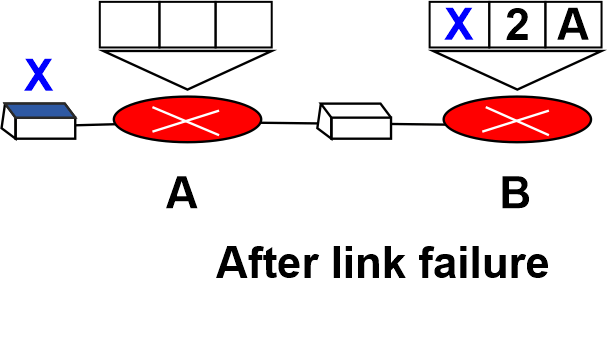
• A system with three nodes is depicted in the figure. Only the elements of the forwarding table required for our discussion have been displayed. Nodes A and B are first able to connect to node X. However, the connection between A and X abruptly breaks down. The table of Node A is altered. Everything will be good if A can quickly transmit its table to B. If B, instead of waiting for A to transmit its forwarding table, sends its forwarding table to A first, the system becomes unstable.

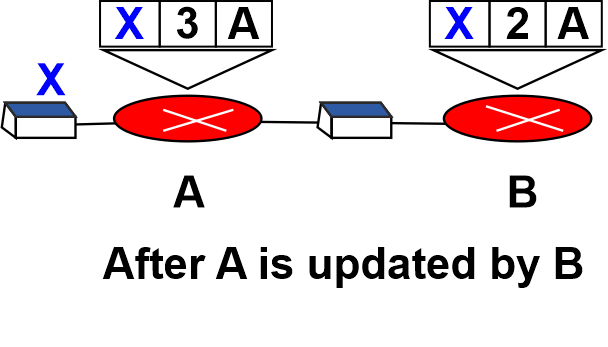
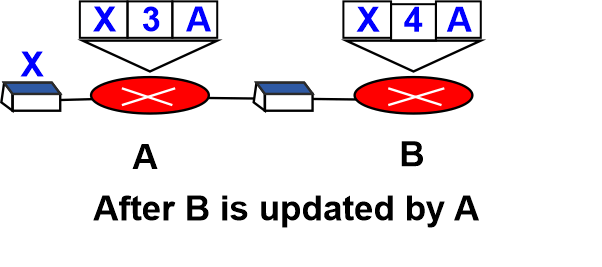
• When Node A receives the update, it instantly updates its forwarding table in the event that B has managed to connect to X. A has just updated B and sent it a fresh message. B has now updated its forwarding table as it believes that something has changed around A. Until it approaches infinity, the price of getting to X rises gradually. Both A and B are aware that X cannot be reached at this time. In contrast, the system is unstable at the present time.

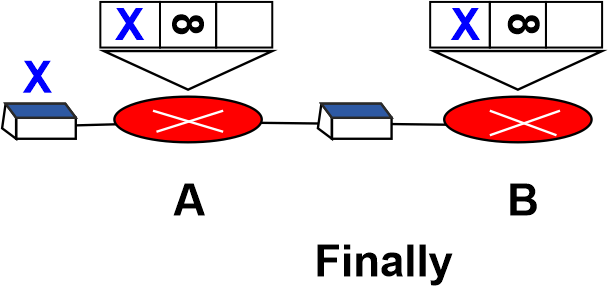
• Node A believes that node B is the path to X, while node B believes that node A is the way to X. When A gets a packet intended for X, the packet first travels to B before returning to A. Similar to this, if B receives a packet meant for X, it travels to A before returning to B. A two-node loop problem is caused by packets bouncing between A and B. There are a few remedies that have been suggested for this form of instability.

The following is the answer to the problem of counting to infinity:

1. Split Horizon
   The split horizon is a method for resolving instability. Each node in this technique delivers a portion of its table across each interface rather than flooding the table through all of them. If node B believes that the best way to go to X is through node A, then node B need not inform node A of this information because it has already been provided by node A (A already knows).
   Confusion is brought on by receiving data from node A, altering it, then sending it back to node A. In our example, node B trims the end of its forwarding table before transmitting it to node A. In this instance, node A maintains a distance to X of infinity. Later, node B similarly makes corrections to its forwarding table when node A transmits it to it. After the initial update, the system is stable because both nodes A and B are aware that X cannot be reached.
2. Poison Reverse
   The split-horizon approach has one disadvantage. If there is no news about a route after a certain amount of time, the corresponding protocol typically employs a timer and instructs the node to remove the route from its table. In the previous example, node A is unable to determine whether node B's decision to remove the route to X from its advertisement to node A is the result of the split-horizon technique (the information came from A) or the fact that B has not recently received any news concerning X.
   In the poison reverse technique, B can still state the value for X, but if the information came from A, it can substitute infinite for the distance as a warning: " Do not utilise this value; you are the source of my knowledge regarding this route."

Note: With the help of split horizon and poison reverse, the two-node instability can be prevented. However, stability cannot be assured if instability occurs between three nodes. The instability between three nodes is referred to as three-node instability