Level Order Traversal of a Binary Tree in Java

The breadth first traversal of a binary tree is also known as the level order traversal of a binary tree in Java.

For the following binary tree: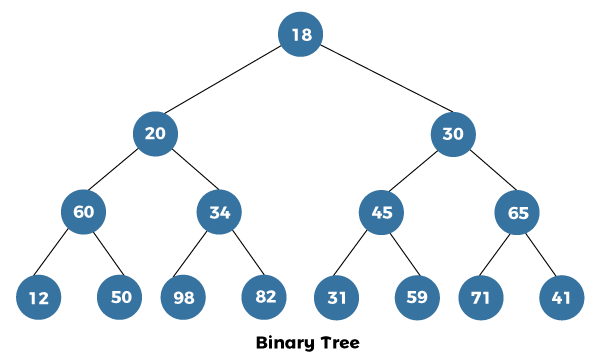

The level order traversal is: 18 20 30 60 34 45 65 12 50 98 82 31 59 71 41

Using Recursion

One can do the level order traversal of a binary tree using recursion. In the recursive approach, we have to take care of the left and right subtrees. The pseudo-code shows the same in more detail.

Pseudo Code of the recursive approach

// Method to display the level order traversal of a binary tree
displayLevelorder(btree)
for h = 1 to height(btree)
   displayCurrentLevel(btree, h);

// Method for displaying all the nodes at the current level
displayCurrentLevel(btree, level)
if btree is NULL, then exit from the method;
if the level is 1, then
    display(btree->val);
else if the level is > 1, then
    displayCurrentLevel(btree->left, level - 1);
    displayCurrentLevel(btree->right, level - 1);

Implementation

Let's implement the level order traversal of the binary tree using the pseudo-code defined above.

FileName: BTreeLevelOrder.java

// A class for creation of nodes of the binary Tree
// nodes of the binary tree contain 
// a left and a right reference
// and a value of the node
class TreeNode 
{
// for holding value of the node
int val;

// for referring to the other nodes
TreeNode left, right;

// constructor of the class TreeNode
// the construct initializes the class fields
public TreeNode(int i)
{
val = i;
right = left = null;
}
}

public class BTreeLevelOrder  
{
// top node i.e. root of the Binary Tree
TreeNode r;

// constructor of the class BTree
public BTreeLevelOrder() { r = null; }

// method for displaying the level order traversal of the binary tree
void displayLevelOrder()
{
int ht = treeHeight(r);
int j;

for (j = 1; j <= ht; j++)
{
displayCurrentLevel(r, j);
}
}

// finding the "height" of the binary tree
// Note that the total number of nodes
// present in the longest path from the topmost node (root node_
// to the leaf node, which is farthest from the root node, gives the
// height of the  tree
int treeHeight(TreeNode r)
{
if (r == null)
{
return 0;
}
else 
{
// finding the height of the left and right subtrees
int lh = treeHeight(r.left);
int rh = treeHeight(r.right);

// picking up the larger one
if (lh > rh)
{
return (lh + 1);
}
else
{
return (rh + 1);
}
}
}

// Printing nodes present in the current level
void displayCurrentLevel(TreeNode r, int l)
{
// null means nothing is there to print
if (r == null)
{
return;
}

// l == 1 means only one node 
// is present in the binary tree
if (l == 1)
{
System.out.print(r.val + " ");
}

// l > 1 means either there are nodes present in
// the left side of the current node or in the 
// right side of the current node or in both sides
// therefore, we have to look in the left as well as in 
// the right side of the current node
else if (l > 1) 
{
displayCurrentLevel(r.left, l - 1);
displayCurrentLevel(r.right, l - 1);
}
}

// main method
public static void main(String argvs[])
{
// creating an object of the class BTreeLevelOrder 
BTreeLevelOrder  tree = new BTreeLevelOrder ();

// root node
tree.r = new TreeNode(18);

// remaining nodes of the tree
tree.r.left = new TreeNode(20);
tree.r.right = new TreeNode(30);
tree.r.left.left = new TreeNode(60);
tree.r.left.right = new TreeNode(34);
tree.r.right.left = new TreeNode(45);
tree.r.right.right = new TreeNode(65);
tree.r.left.left.left = new TreeNode(12);
tree.r.left.left.right = new TreeNode(50);
tree.r.left.right.left = new TreeNode(98);
tree.r.left.right.right = new TreeNode(82);
tree.r.right.left.left = new TreeNode(31);
tree.r.right.left.right = new TreeNode(59);
tree.r.right.right.left = new TreeNode(71);
tree.r.right.right.right = new TreeNode(41);


System.out.println("Level order traversal of binary tree is ");
tree.displayLevelOrder();
}
}

Output:

Level order traversal of binary tree is 
18 20 30 60 34 45 65 12 50 98 82 31 59 71 41

Time Complexity: The time complexity of the program is O(n^2) in the worst case, where n is the total number of nodes of a binary tree. Note that the worst scenario occurs when the tree is skewed.

Space Complexity: The space complexity of the program is O(n) in the worst case, where n is the total number of nodes of a binary tree. Note that the worst scenario occurs when the tree is skewed. For a skewed tree, the displayCurrentLevel() method uses the O(n) space for the call stack. In our case, the tree is balanced; therefore, the space used is O(log(n)), which is the height of a balanced tree.

Using Queue

One can also accomplish the level order traversal of a binary tree using a queue. Using queue, first, we put all of the children of a node in a queue. The left child is put first in the queue, followed by the right child. As a queue works on the FIFO (First In First Out) principle, the left child comes out first, then the right child, and thus, the level ordered traversal of the tree is achieved. For better understanding, let's observe the pseudo-code then its implementation.

Pseudo Code for traversal using queue

displayLevelorder(tree)
1) Create a queue that is empty. Let's say the queue is que
2) tNode = r // starting from the root
3) Iterate until the tNode is not NULL
    a) display the tNode->val.
    b) enqueue the children of the tNode
      (First the left child and then the right child) into que
    c) A node n is then dequeue from the queue (que)

Implementation

Let's implement the level order traversal of the binary tree using the pseudo-code defined above.

FileName: BTreeLevelOrder1.java

// importing the Queue and LinkedList classes
// that are required in the program 
import java.util.Queue;
import java.util.LinkedList;


// A class for creation of nodes of the binary tree
// nodes of the binary tree contain 
// a left and a right reference
// and a value of the node
class TreeNode 
{
// for holding value of the node
int val;

// for referring to the other nodes
TreeNode left, right;

// constructor of the class TreeNode
// the construct initializes the class fields
public TreeNode(int i)
{
val = i;
right = left = null;
}
}

// class that prints the level order 
// traversal using queue
public class BTreeLevelOrder1 
{

// top node, i.e. root of the Binary Tree
TreeNode r;

// constructor of the class BTree
public BTreeLevelOrder1() { r = null; }

// method for displaying the level order traversal of the binary tree
void displayLevelOrder()
{
// creating a empty queue
Queue<TreeNode> que = new LinkedList<TreeNode>();

// adding the node
que.add(r);

while (!que.isEmpty()) 
{
// removing the front node from the queue
TreeNode tNode = que.poll();

// print the value of the removed node
System.out.print(tNode.val + " ");

// if the left child is present, enqueue the left child 
if (tNode.left != null) 
{
que.add(tNode.left);
}

// if the right child is present, enqueue the right child too
if (tNode.right != null) 
{
que.add(tNode.right);
}
}
}

// main method
public static void main(String argvs[])
{
// creating an object of the class BTreeLevelOrder1 
BTreeLevelOrder1  tree = new BTreeLevelOrder1();

// root node
tree.r = new TreeNode(18);

// remaining nodes of the tree
tree.r.left = new TreeNode(20);
tree.r.right = new TreeNode(30);
tree.r.left.left = new TreeNode(60);
tree.r.left.right = new TreeNode(34);
tree.r.right.left = new TreeNode(45);
tree.r.right.right = new TreeNode(65);
tree.r.left.left.left = new TreeNode(12);
tree.r.left.left.right = new TreeNode(50);
tree.r.left.right.left = new TreeNode(98);
tree.r.left.right.right = new TreeNode(82);
tree.r.right.left.left = new TreeNode(31);
tree.r.right.left.right = new TreeNode(59);
tree.r.right.right.left = new TreeNode(71);
tree.r.right.right.right = new TreeNode(41);


System.out.println("Level order traversal of binary tree is: ");
tree.displayLevelOrder();
}
}

Output:

Level order traversal of binary tree is:
18 20 30 60 34 45 65 12 50 98 82 31 59 71 41

Time Complexity: The time complexity of the program is O(n), where n is the total number of nodes of a binary tree.

Space Complexity: The space complexity of the program is also O(n), where n is the total number of nodes of a binary tree.

Comparison of Both the Approaches

By comparing the time and space complexities of both the approaches, we find the using queue; we achieve the result much quicker. Also, the time complexity, as well as the space complexity of the queue program, is not dependent on the arrangement of nodes. It means, even if the tree is skewed, the time and space complexity of the program does not change, and such thing is not possible with the recursive approach. In the recursive approach, it matters a lot on the arrangement of nodes of the tree.

Next TopicBully algorithm in Java

← prev next →