Maximum Rectangular Area in a Histogram in Java

In this section, we will see how one can compute the maximum rectangular area in the histogram.

What is maximum rectangular area in the histogram?

The maximum rectangle that has to be created should be made of continuous bars. For the sake of simplicity, we will assume that the width of each bar is 1.

For example, for the following histogram that has 7 bars of the heights {7, 3, 6, 5, 6, 2, 7}, the maximum rectangular area, which is possible, is 15. The maximum area is highlighted in yellow color.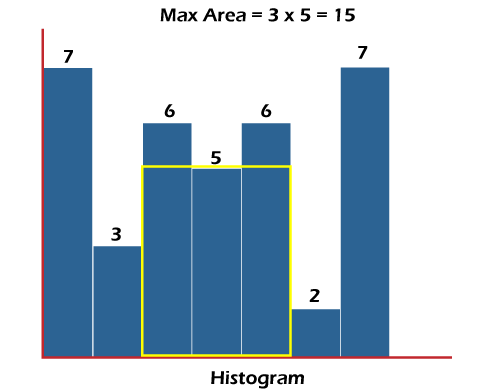

Maximum Rectangular Area in a Histogram in Java

Let's discuss the various approaches to solve this problem.

Naïve Approach

In this approach, we will consider each bar one by one as the starting point, and from the starting point, we will compute the rectangular area each time by taking the next coming bar one by one. Every time we compute the rectangular area, we compare it with the current maximum area (initially, the maximum area is initialized with 0).

FileName: LargestRectArea.java

public class LargestRectArea 
{

// a method that finds the 
// minimum between a & b
int findMin(int a, int b)
{
  int min = (a > b) ? b : a; 
  return min;
}

// a method that finds the 
// maximum between a & b
int findMax(int a, int b)
{
  int max = (a > b) ? a : b; 
  return max;
}

// the main method
public static void main(String argvs[])
{
// creating an object of the class LargestRectArea
LargestRectArea obj = new LargestRectArea();

// input array in which each element represents the
// height of the bar of the histogram
int arr[] = {7, 3, 6, 5, 6, 2, 7};
int size = arr.length;

int maxArea = 0;

for(int i = 0; i < size; i++)
{
// arr[i] is the first bar of the 
// maximum rectangular area
int temp = arr[i];
maxArea = obj.findMax(temp, maxArea);
for(int j = i + 1; j < size; j++)
{
    temp = obj.findMin(temp, arr[j]);
    maxArea = obj.findMax(maxArea, temp * (j - i + 1));
}
}
System.out.println("The maximum rectangular area is: " + maxArea);
}
}

Output:

The maximum rectangular area is: 15

Time Complexity: In the above program, we have used the nested for-loops of degree 2. Therefore, the total complexity of the above program is O(n²), where n is the total number of elements present in the input array.

Divide and Conquer Approach

The concept is to find the index of a value in the input array that is minimum. Once we have found the index of the value that is minimum, the maximum area is the maximum of the following three values.

Area that is maximum on the left side of the minimum value (excluding the minimum value)
Area that is maximum on the right side of the minimum value (excluding the minimum value).
Total count of bars multiplied by the minimum bar value.

Observe the following program.

import java.util.*;

public class LargestRectArea1
{
static int hist[];
static int segTree[];

// A utility method to find the minimum of the three integers
public int max(int a, int b, int c)
{ return Math.max(Math.max(a, b), c); }

// A utility method to get the minimum of the two numbers in the hist[]
public int findMin(int a, int b)
{
if (a == -1)
{ return b; }
if (b == -1) { return a; }
return (hist[a] < hist[b]) ? a : b;
}

// A utility method to retrieve the middle idx using the corner indices.
public int findMid(int s, int e)
{ return s + (e - s) / 2; }

// A recursive method for getting the index of the minimum value in the provided range of
// the indices. The following are the different parameters for this method.

// hist - The input array for which the segment tree is made
// segTree - segment tree pointer
// idx -. It represents the curr node index in the seg tree. Initially zero is passed as the 
// root is always at the index zero
// si & ei - si = starting index and ei = ending index of the segment as shown by the curr // node, i.e., si[idx]
// qs & qe - Query Start = qs & Query End = qe 
public int findIndexUtility( int si, int ei, int qs, int qe, int idx)
{
// If the segment of this node is in the portion of the provided range, then send the
// minimum value of segment
if (qs <= si && qe >= ei)
{
return segTree[idx];
}

// If the segment of this node is outside the given range
if (ei < qs || si > qe)
{
return -1;
}

// If the part of this segment is overlapping with the provided range
int mid = findMid(si, ei);
return findMin( findIndexUtility(si, mid, qs, qe, 2 * idx + 1),
	findIndexUtility( mid + 1, ei, qs, qe, 2 * idx + 2));
}

// the method returns the index of the minimum element in the range from the index qs (query begin) to
// query end (qe). It uses the findIndexUtil() method
public int returnIndex( int s, int qb, int qe)
{
// Check for the out of range input values
if (qb < 0 || qe > s - 1 || qb > qe)
{
System.out.print("The given input is not valid");
return -1;
}

return findIndexUtility( 0, s - 1, qb, qe, 0);
}

// A recursive method that makes the Segment Tree for the hist[s ... e].
// si is the index of the current node in the segment tree segTree
public int constructSTUtililty(int s, int e, int si)
{
// When there is only one element in the tree, keep it in the curr node of
// the segment tree and then return
if (s == e)
{
return (segTree[si] = s);
}

// When more than one element is present, we have to do the recursion for the right and
// the left subtrees and store the minimum of the two values into this node
int mid = findMid(s, e);
segTree[si] = findMin(constructSTUtililty(s, mid, si * 2 + 1),
		constructSTUtililty(mid + 1, e, si * 2 + 2));
return segTree[si];
}

// method for making the seg tree from the given array. The method
// that assigns the memory for the segment tree and invokes the constructSTUtililty() 
// method for
// filling the memory that is allocated
public void constructSegTree(int s)
{
// Allocating memory for the segment tree
int x = (int)(Math.ceil(Math.log(s))); // Height of the segment tree
int maxSize = 2 * (int)Math.pow(2, x) - 1; // The Maximum size of the segment tree
segTree = new int[maxSize * 2];

constructSTUtililty( 0, s - 1, 0);

}

// A method that recursively looks for the rectangular area that is maximum.
// It uses the segment tree 'segTree' to look for the minimum value in hist[l ... r]
public int findMaxAreaRec( int s, int lt, int rt)
{
// handling the Base cases
if (lt > rt)  return Integer.MIN_VALUE;
if (lt == rt)  return hist[lt];

// Find index of the minimum value in given range
// This takes O(Logn)time
int i = returnIndex(s, lt, rt);

// Returning the maximum of following the three possible cases:
//   a) The maximum area in the left of the minimum value (excluding the minimum)
//   a) The maximum area in the right of the minimum value (excluding the minimum)
//   c) The maximum area including the minimum 
return max(findMaxAreaRec(s, lt, i - 1), findMaxAreaRec( s, i + 1, rt), (rt - lt + 1) * (hist[i]));
}

// The method for computing the max rect area
public int computeMaxArea( int s)
{
// Constructing the segment tree from the provided array. It takes O(n) time
constructSegTree(s);

// Using the utility method that uses recursion for finding the
// maximum area
return findMaxAreaRec(s, 0, s - 1);
}

// main method
public static void main(String[] argvs)
{
int[] arr = {7, 2, 6, 5, 6, 2, 7};
int s = arr.length;
hist = new int[s];
LargestRectArea1 obj = new LargestRectArea1();
hist = arr;
System.out.println("The maximum rectangular area is: " + obj.computeMaxArea(s));
}
}

Output:

The maximum rectangular area is: 15

Time Complexity: In the above program, the time complexity is dependent on two things: one is the segment tree, and the second is finding the maximum rectangular area. The time complexity consumed in building the segment tree is O(n) and for finding the maximum rectangular area, the time complexity is O(log(n)). Thus, the time complexity becomes O(n) + O(n * log(n)), and asymptotically the time complexity becomes O(n * log(n)), where n is the total number of elements present in the input array.

If we compare the above two programs, we find that the latter one is more optimized as it takes less time to solve the problem. However, we can even optimize it furthermore. Let's see it in the following approach.

Approach: Using Stack

Let's see the algorithm for finding the rectangular area using stack.

Step 1: Create a stack for pushing and popping elements.

Step 2: Begin from the first bar, and perform the following task for every bar "histArr[j]" where 'j' varies from 0 to s - 1.

If the stack is containing zero elements or histArr[ij] is longer than the bar present at the top of the stack, then push 'j' to the stack.
If the current bar is shorter than the bar present at the top of stack, then keep popping the bars from the top of stack until the bar present at the top of the stack is larger. Assume that the removed bar is histArr[top]. Compute the rectangle area with histArr[top] as the smallest bar. For the histArr[top], the 'left index' is the previous (previous to top) bar in the stack, and the 'right index' is 'j' (the current index).

Step 3: If the stack is containing some bars, pop all the bars one by one from the stack and repeat step 2(ii) for every removed bar.

FileName: LargestRectArea2.java

// import statement
import java.util.Stack;

public class LargestRectArea2
{
// The main method for computing the maximum rect area using the input
// histogram array with s bars
public int findMaxArea(int histArr[], int s)
{
// Creating an empty stack. The stack keeps indices of the histArr[] array
// The bars kept in the stack are in increasing order as per their heights
Stack<Integer> stk = new Stack<>();

int maxArea = 0; // Initializing the max area
int top; // for keeping the top of the stack
int areaWithTop; // for keeping the area with the bar at the top as the smallest bar

// Run through all bars of given histogram
int j = 0;
while (j < s)
{
// If the bar is longer than the bar present at the top of the stack, then push the bar to //the stack
if (stk.empty() || histArr[stk.peek()] <= histArr[j])
stk.push(j++);

// If the bar is lower than the top of the stack, then compute the area of the rectangle
// with the top of the stack as the min-height bar. 'j' is the right index for the 
// top and the element before the top in the stack is the 'left index'
else
{
top = stk.peek(); // storing the index at the top
stk.pop(); // popping the top

// computing the area with histArr[top] stack as the smallest bar
areaWithTop = histArr[top] * (stk.empty() ? j : j - stk.peek() - 1);

// updating the maximum area, if requried
if (maxArea < areaWithTop)
{
maxArea = areaWithTop;
}
}
}

// Now popping the left bars from the stack and computing the area with each bar
// that is popped as the bar that is smallest
while (stk.empty() == false)
{
top = stk.peek();
stk.pop();
areaWithTop = histArr[top] * (stk.empty() ? j : j - stk.peek() - 1);

if (maxArea < areaWithTop)
maxArea = areaWithTop;
}

return maxArea;

}

// Driver method to test above methods
public static void main(String[] args)
{
int[] histArr = {7, 2, 6, 5, 6, 2, 7};
int s = histArr.length; // computing size

// creating an object of the class LargestRectArea2
LargestRectArea2 obj = new LargestRectArea2();
System.out.println("The maximum rectangular area is: " + obj.findMaxArea(histArr, s));
}
}

Output:

The maximum rectangular area is: 15

By Using Auxiliary Arrays

Another approach is to find the previous smaller and the next smaller bar, for every bar present in the histogram, and it will be achieved using two auxiliary arrays. See the following algorithm.

Step 1: First, we take two auxiliary arrays leftSmaller[] and rightSmaller[] and initialize them with a negative number and n, respectively.

Step 2: For each element, we keep the index of the next smaller and the previous smaller element in rightSmaller[] and leftSmaller[] arrays, respectively. It takes O(n) time.

Step 3: For each bar, we compute the area by taking the j^th bar as the shortest in the range leftSmaller[j] and rightSmaller[j] and multiplying it with the difference of leftSmaller[j] and rightSmaller[j].

Step 4: The maximum area can be computed by comparing the area for each bar. The area for the different bars is computed in step 3.

FileName: LargestRectArea3.java

// import statement
import java.util.Stack;


public class LargestRectArea3
{

// method for finding the maximum rectangular area in the given histogram.
public int findMaxArea(int a[], int s)
{
// creating an empty stack here
Stack<Integer> stk = new Stack<>();

// we push a negative number to the stack as for some of the bars there is a possibility that the previous smaller 
// bar is absent in the input array. In our case it is -1.
stk.push(-1);
int maxArea = a[0];
// We declare the leftSmaller and the rightSmaller array of the size s and intializing them with -1 and s as their default value.
// leftSmaller[j] keeps the index of the previous smaller bar for the jth bar.
// rightSmaller[j] keeps the index of the next smaller bar for the jth bar.
int leftSmaller[] = new int[s];
int rightSmaller[] = new int[s];
for (int j = 0; j < s; j++)
{
leftSmaller[j] = -1;
rightSmaller[j] = s;
}

int j = 0;
while (j < s)
{
while(!stk.empty() && stk.peek() != -1 && a[j] < a[stk.peek()])
{
// if the current bar is shorter than the bar with the index kept on the top
// of the stack then, pop the top bar and keep the current bar index as the rightSmaller
// for the bar that is popped bar.
rightSmaller[stk.peek()] = (int)j;
stk.pop();
}
if(j > 0 && a[j] == a[(j - 1)])
{
// use this condition to escape the loop that is unnecessary to look for the leftSmaller.
// since the previous bar is the same as the current element, 
// the leftSmaller bar is the same for both, always.
leftSmaller[j] = leftSmaller[(int)(j - 1)];
}
else
{
// bar with the stored index at the top of the stack is always shorter
// than the current bar.
// Hence, the leftSmaller[j] will always be on stk.top().
leftSmaller[j] = stk.peek();
}
stk.push(j);
j = j + 1;
}


for(j = 0; j < s; j++)
{
// computing the area with every bar as the shortest bar in its range and then 
// do the comparison it with the previously computed area. Using this way
// one can get the maximum area from this.
maxArea = Math.max(maxArea, a[j] * (rightSmaller[j] - leftSmaller[j] - 1));
}

return maxArea;
}

// main method
public static void main(String argvs[])
{
int[] histArr = {7, 2, 6, 5, 6, 2, 7};
int size = histArr.length; // computing size

LargestRectArea3 obj = new LargestRectArea3();
System.out.println("The maximum rectangular area is: " + obj.findMaxArea(histArr, size));
}
}

Output: