Polygonal Number in JavaA polygonal number is a number in mathematics represented by dots or pebbles organized in the shape of a regular polygon. The dots are referred to as alphas (units). These are two-dimensional figurate integers of a particular sort. Polygonal numbers are the numbers that represent dots organized in a geometric pattern. Beginning with a common point and expanding outward, the number of dots used in succeeding polygons grows. As the figure develops in size, the number of dots used to form it expands predictably. The polygonal number starts from 1 and is equal to the vertices of the geometric pattern. It finds a polygonal number of triangles, squares, and pentagon patterns. The polygonal number increases with the adjacent side of the figure. A polygonal number may be represented by regular and discrete geometric patterns with evenly spaced points. It is a polygonal, polyhedral, or polytopic number if the arrangement of points results in a regular polygon, regular polyhedron, or regular polytope. The polygonal number increases as long as possible using Java programming language. Type of the Polygonal NumberThe shape must be a 2-dimensional diagrams get a polygonal number. There are some basic diagrams to get polygonal numbers using Java. The triangle and square are the most usable figure to find polygonal numbers. We can use hexagon and pentagon diagrams to get a polygonal number. Triangular Polygonal NumberThe triangle gets 1 value for the first term and 3 values for the second term of the polygonal number. It increases by the three sides of the triangle. We can calculate the triangular polygonal number by using the following formula. The polygonal numbers of triangular shape: 1, 3, 6, 10, 15, ... Square Polygonal NumberThe square gets 1 value for the first term and 4 values for the second term of the polygonal number. It increases by the four sides of the square. We can calculate the square polygonal number by using the following formula. Pentagon Polygonal NumberThe square gets 1 value for the first term and 5 values for the second term of the polygonal number. It increases by the five sides of the pentagon. We can calculate the pentagon polygonal number by using the following formula. The pentagonal polygonal numbers: 1, 5, 12, 22, 35! Hexagon Polygonal NumberThe square gets 1 value for the first term and 6 values for the second term of the polygonal number. It increases by the six sides of the hexagon. We can calculate the hexagon polygonal number by using the following formula. The hexagonal polygonal numbers: 1, 6, 15, 28, 45, ... Polygonal Number Java ProgramsThe following examples show the working procedure of the polygonal number in the Java language. Java Program to Find the Polygonal NumberBasicpolygonalnumber.java Output: 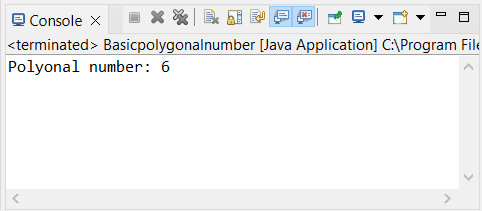
Java Program to Find the Square Polygonal NumberSquarepolygonalnumber.java Output: 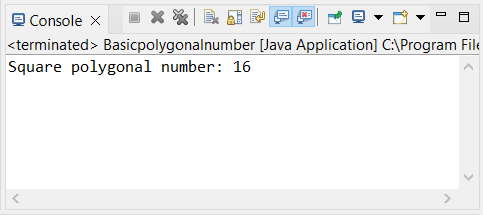
Java Program to Find the Pentagon Polygonal NumbersPentagonepolygonalnumber.java Output: 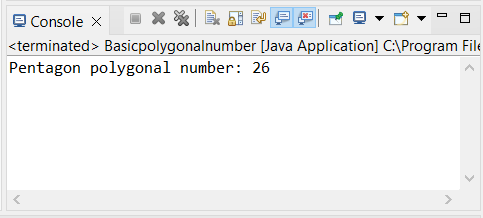
Java Program to Find the Hexagon Polygonal NumbersHexagonepolygonalnumber.java Output: 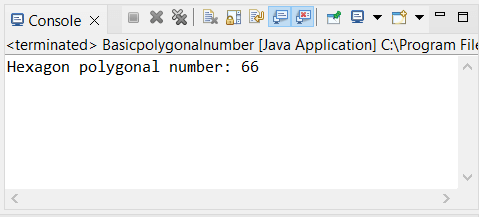
Polygonal Number of the GeometricThe example uses a scanner for the trigonometric figure and the polygonal number. The scanner helps to choose the required side and time of the number. The example contains the formula for triangle, square, pentagonal, and required diagram. The formula finds a polygonal number of the figure. Polygonalnumber.java Output: 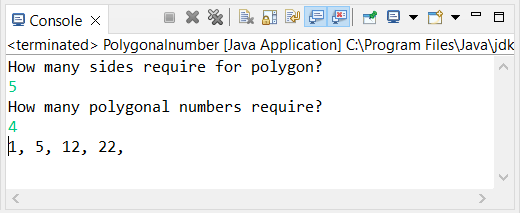
Java Program to Find the Central Polygonal NumberThe following example finds a sixth number of the central polygonal number using Java. We can find a n-th number of the central polygonal using Java programming language. Centralpolygonalnumber.java Output: 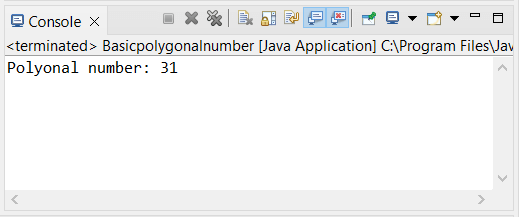
ConclusionJava language requires a formula to get polygonal numbers. The number helps to find the order of the vertices. The vertices help get the point and extended diagram of the trigonometric figure. The polygonal number in Java helps to reduce trigonometric calculation. Java programming calculates polygonal numbers as per requirement. We can calculate the required shape and number of polygonal. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










