Picture Analogies 311) The first pair is complete, and the second pair is incomplete. Select one picture out of four pictures given below that will complete the second pair so that pictures in the second pair are related to each other in the same way as the pictures in the first pair are related to each other.   Answer: B Explanation: A penny is to a dollar as a house is to a building. It indicates a unit and a group of units. A penny is a unit of a dollar, and a house is a unit of a residential building. 12) The first pair is complete, while the second pair is not complete. Which picture out of four pictures given below will complete the second pair so that pictures in the second pair are related to each other in the same way as the pictures in the first pair are related to each other?   Answer: D Explanation: A house is to a tent as a car is to a wagon. The house is a more advanced or sophisticated form of a shelter than a tent house, similarly, a car is an advanced or more sophisticated mode of transportation than a wagon. So, wagon will complete the second pair. 13) The first pair is complete, whereas the second pair is not complete. Select one picture out of four pictures given below that will complete the second pair so that pictures in the second pair share the same relationship as the pictures in the first pair.   Answer: C Explanation: Bread is to a knife as a log of wood is to an ax. The knife is used to cut bread into slices; similarly, an ax is used to chop a log of wood. So, the log of wood will complete the second pair. 14) The first pair is complete, whereas the second pair is not complete. Select one picture out of four pictures given below that will complete the second pair so that pictures in the second pair are related to each other in the same way as the pictures in the first pair are related to each other.   Answer: D Explanation: A hose is to a firefighter as a syringe is to a nurse. It indicates the tools used in a trade. A firefighter uses a hose to extinguish the fire, and a nurse uses a syringe to inject the vaccine. So, the picture of a nurse will complete the pair.s 15. The first pair is complete, whereas the second pair is not complete. Select one picture out of four pictures given below that will complete the second pair so that pictures in the second pair have the same relationship with each other as the pictures in the first pair.  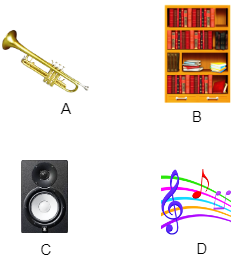 Answer: A Explanation: A newspaper is to a book as a tabla (hand drum) is to a trumpet. The newspaper and book are meant to be read, and trumpet and tabla are intended to be played by musicians. So, a trumpet will complete the second pair. Picture Analogies 1 Picture Analogies 2
Next TopicRule Detection 1
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










